\(f(x) = -x^2 +a*x -2\)
Bestimme a so, dass die Nullstellen den Abstand 4 haben.
\( -x^2 +a*x -2=0\)
\( x^2 -a*x =-2\)
\( (x -\frac{1}{2}a)^2 =-2+\frac{1}{4}*a^2\)
1.)
\( x -\frac{1}{2}a =\sqrt{\frac{1}{4}*a^2-2}\)
\( x_1 = \frac{1}{2}a+\sqrt{\frac{1}{4}*a^2-2}\)
2.)
\( x -\frac{1}{2}a =-\sqrt{\frac{1}{4}*a^2-2}\)
\( x_2 = \frac{1}{2}a-\sqrt{\frac{1}{4}*a^2-2}\)
\(x_2-x_1=\frac{1}{2}a-\sqrt{\frac{1}{4}*a^2-2}-( \frac{1}{2}a+\sqrt{\frac{1}{4}*a^2-2})=4\)
\(\sqrt{\frac{1}{4}*a^2-2}=-2\)
\(\frac{1}{4}*a^2-2=4\)
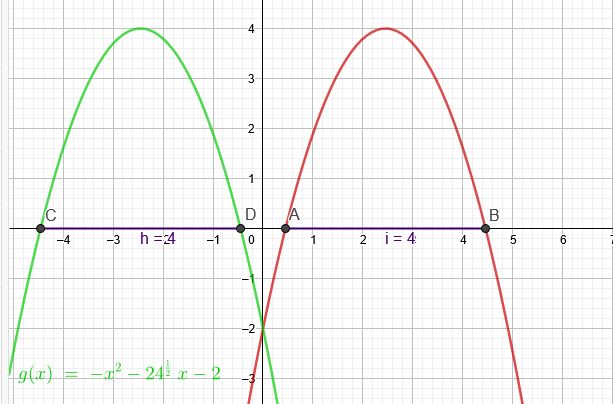
\(a^2=24\) →\(a_1= \sqrt{24} \) →\(a_2= -\sqrt{24} \)
1.) \(f(x) = -x^2 +\sqrt{24} *x -2\)
2.) \(g(x) = -x^2 -\sqrt{24} *x -2\)