Mit Näherungsverfahren kenne ich mich gar nicht aus.
\(-x^4-x^3-6x^2+x=x^4+3x^2-1\)
\(-2x^4-x^3-9x^2+x+1=0\)
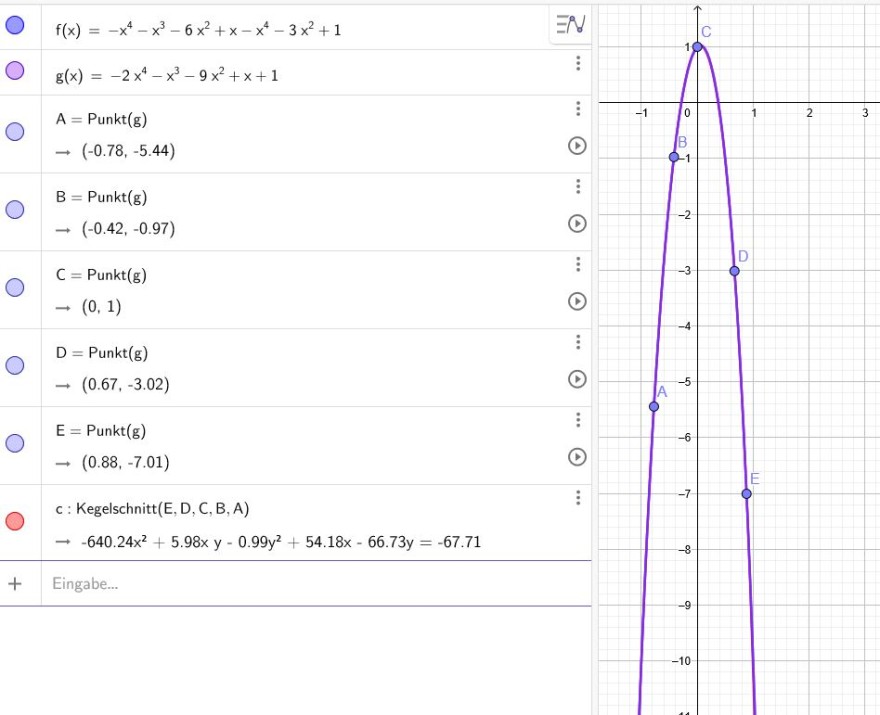
Mit Geogebra kommt ein Kegelschnitt heraus:
\(-640,24x^2+5,98xy-0,99y^2+54,18x-66,73y=-67,71\)
Nullstellen \(y=0\)
\(-640,24x^2+54,18x=-67,71\)
mit Wolfram:
\(x_1≈-0,28563\)
\(x_2≈0,370257\)