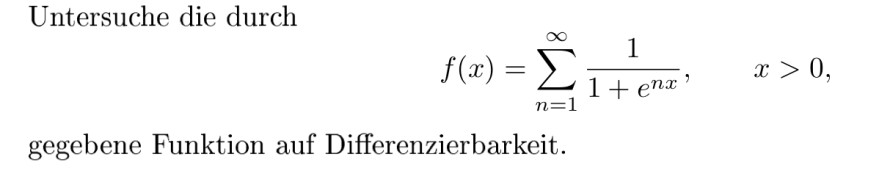
Text erkannt:
Untersuche die durch
\( f(x)=\sum \limits_{n=1}^{\infty} \frac{1}{1+e^{n x}}, \quad x>0 \)
gegebene Funktion auf Differenzierbarkeit.
Mein Ansatz war, dass f(x) alternativ als Limes einer Funktionenfolge definiert werden kann. So könnte ich doch mit Konvergenz die Differenzierbarkeit begründen.
1. ist mein Ansatz und die Folgerung korrekt?
2. Wie finde ich eine alternative Definition für f mithilfe von Funktionenfolgen?