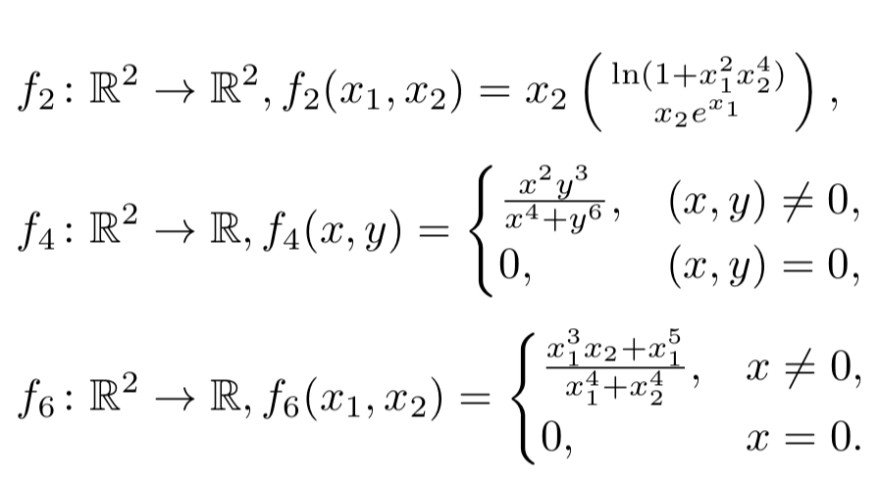
Text erkannt:
\( \begin{array}{l}f_{2}: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}, f_{2}\left(x_{1}, x_{2}\right)=x_{2}\left(\begin{array}{cc}\ln \left(1+x_{1}^{2} x_{2}^{4}\right) \\ x_{2} e^{x_{1}}\end{array}\right), \\ f_{4}: \mathbb{R}^{2} \rightarrow \mathbb{R}, f_{4}(x, y)=\left\{\begin{array}{ll}\frac{x^{2} y^{3}}{x^{4}+y^{6}}, & (x, y) \neq 0, \\ 0, & (x, y)=0,\end{array}\right. \\ f_{6}: \mathbb{R}^{2} \rightarrow \mathbb{R}, f_{6}\left(x_{1}, x_{2}\right)=\left\{\begin{array}{ll}\frac{x_{1}^{3} x_{2}+x_{1}^{5}}{x_{1}^{4}+x_{2}^{4}}, & x \neq 0, \\ 0, & x=0 .\end{array}\right.\end{array} \)
Aufgabe: Untersuche die Funktionen auf Differenzierbarkeit und bestimme, wo möglich ihre Ableitungen.
Wie gehe ich bei den drei Funktionen am besten vor? Also welches „Kriterium“ bzw Methode wäre hier am besten?