Bestimmen Sie die Normalform dieser Quadrik.

Question

Aufgabe:

Gegeben ist die Quadrik
23232√√ Q= x∈R : 2x1+2x2−x1x2− 18x1+ 2x2+2=0 .
Bestimmen Sie die Normalform dieser Quadrik.

Text erkannt:

Gegeben ist die Quadrik
\( Q=\left\{x \in \mathbb{R}^{2}: \frac{3}{2} x_{1}^{2}+\frac{3}{2} x_{2}^{2}-x_{1} x_{2}-\sqrt{18} x_{1}+\sqrt{2} x_{2}+2=0\right\} . \)
Bestimmen Sie die Normalform dieser Quadrik.

Answer 1

Hast Du konkrete Fragen? BItte

siehe https://www.geogebra.org/m/BpqJ28eP#chapter/367809

da kannst Du die grundsätzlichen Schritte nachlesen.

Wegen der Wurzeln wäre die kompakte Form in homogenen Koordinaten besser geeignet

Drehen in achsenparalle Lage und verschieben in Ursprung

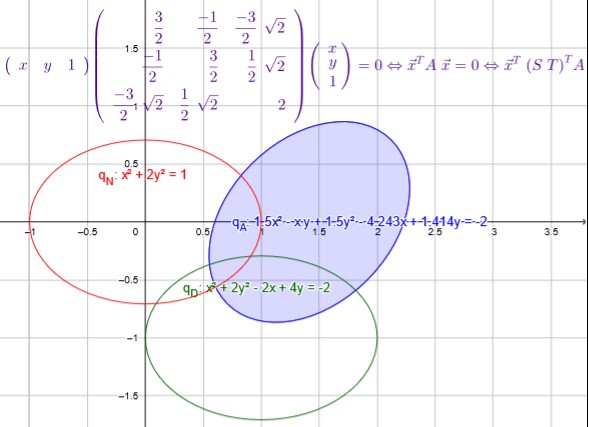
\( \left\{ \left(\begin{array}{rrr}x&y&1\\\end{array}\right) \, \left(\begin{array}{rrr}\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}&0\\\frac{-1}{\sqrt{2}}&\frac{1}{\sqrt{2}}&0\\\sqrt{2}&0&1\\\end{array}\right) \, \left(\begin{array}{rrr}\frac{3}{2}&\frac{-1}{2}&\frac{-3}{2} \; \sqrt{2}\\\frac{-1}{2}&\frac{3}{2}&\frac{1}{2} \; \sqrt{2}\\\frac{-3}{2} \; \sqrt{2}&\frac{1}{2} \; \sqrt{2}&2\\\end{array}\right) \, \left(\begin{array}{rrr}\frac{1}{\sqrt{2}}&\frac{-1}{\sqrt{2}}&\sqrt{2}\\\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}&0\\0&0&1\\\end{array}\right) \, \left(\begin{array}{r}x\\y\\1\\\end{array}\right) \right\} \)

\(q_{N}: \, x^{2} + 2 \; y^{2} - 1 = 0\)