Polynomdivision mit rationalen Funktionen

Question

Aufgabe: Darstellung rationaler Funktionen

Zeigen Sie unter Ausnutzung von Polynomdivision, dass Sie die rationale Funktion p(x)/q(x) mit (siehe Foto)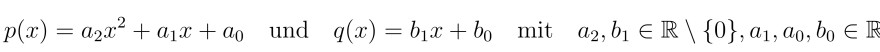 

Text erkannt:

\( p(x)=a_{2} x^{2}+a_{1} x+a_{0} \quad \) und \( \quad q(x)=b_{1} x+b_{0} \quad \) mit \( \quad a_{2}, b_{1} \in \mathbb{R} \backslash\{0\}, a_{1}, a_{0}, b_{0} \in \mathbb{R} \)

Problem/Ansatz: Komme nicht weiter bei der polynomdivision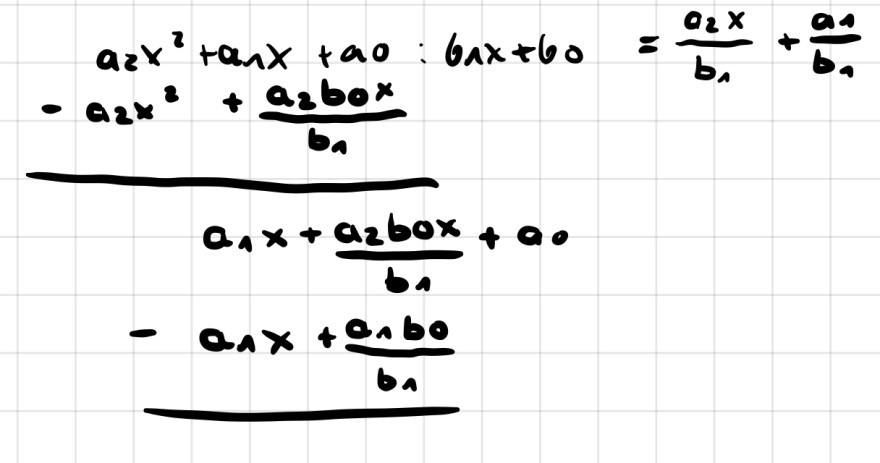

Text erkannt:

\( \begin{array}{l}a_{2} x^{2}+a_{1} x+a_{0}: b_{1} x+b 0=\frac{a_{2} x}{b_{1}}+\frac{a_{1}}{b_{1}} \\ -a_{2} x^{2}+\frac{a_{2} b_{0} x}{b_{1}} \\ a_{1} x+\frac{a_{2} b_{0} x}{b_{1}}+a_{0} \\ -a_{1 x}+\frac{\sigma_{1} b_{0}}{b_{1}} \\\end{array} \)

Comments

Ich sehe da als "Aufgabenstellung" nicht einmal einen vollständigen Satz.

Zeigen Sie ..... dass ..... WAS ?

---

Naja wir sollen hiervon die Polynomdivision durchführen und dann ich die Form p(x) = h(x) + r(x)/q(x) bringen. r(x) ist der Rest der übrig bleibt bei der Division und h(x) das Ergebnis der Polynomdivision

---

Wenn du die Klammern, die um die Subtrahenden gehören, hinschreiben würdest, siehst du vielleicht, welche Fehler du gemacht hast.

---

Schon in Dividend und Divisor fehlen Klammern.

---

Sorry, da bin ich gerade raus, welche Klammern denn?, also die um a2 ... und b1x ...) ?

---

Da kann man dir nur noch im persönlichen Gespräch helfen.

Answer 1

(a·x^2 + b·x + c)/(p·x + q) = a/p·x + (b·p - a·q)/p^2 + (a·q^2 - b·p·q + c·p^2)/p^2 / (p·x + q)

h(x) = a/p·x + (b·p - a·q)/p^2

r(x) = (a·q^2 - b·p·q + c·p^2)/p^2

Comments

Hallo erstmal vielen Dank, aber was wäre denn genau bei meinem Ansatz falsch

---

Naja wenn du nicht siehst das bei dem a2b0/b1 einmal ein x steht und dann ein x fehlt und du das dann vermutlich zu 0 subtrahierst ist das eben verkehrt.

Aber das mit den fehlenden Klammern hast du ja auch schon nicht verstanden.