Ich mache dir mal das Beispiel
f'(x) = 0.2·x^3 - 0.8·x^2 - 0.8·x + 3.2
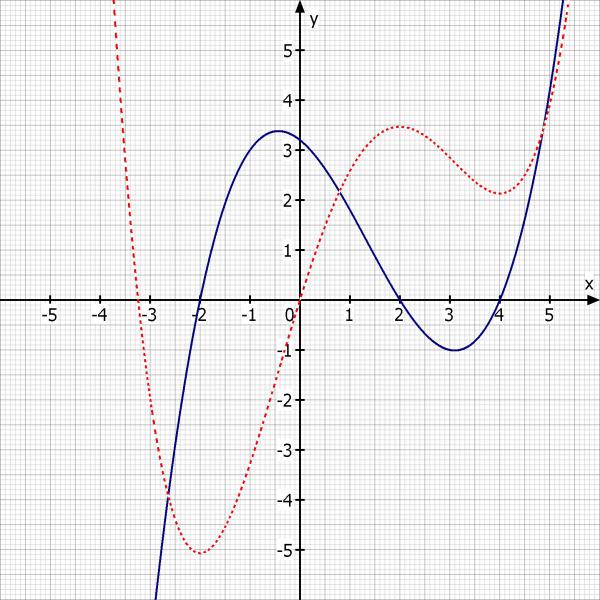
Hier siehst du in blau die Funktion f'(x) und in rot die gesuchte Funktion f(x).
Nullstellen der Gegebenen Funktion werden zu Hoch, Tief oder Sattelpunkten der Stammfunktion.
Hoch und Tiefpunkte werden zu Wendestellen der Stammfunktion.
Genauer kann man die Werte abschätzen wenn man dann noch die Flächen unter den Graphen berechnet. Das braucht man in der regel aber nicht weil es nur skizziert werden soll. D.h. einheiten bleiben i.d.R. unberücksichtigt.
Was du noch wissen solltest ist das die gesuchte Stammfunktion ein Grad höher ist. D.h. wenn meine blaue Funktion vom dritten Grad ist wird die Stammfunktion eine vom Grad 4 sein.