Wenn eine Menge in einem Metrikraum kompakt ist, muss jede Folge in der Menge eine konvergente Teilfolge haben, deren Grenzwert auch in der Menge liegt.
Konstruierst du nun eine Folge so wie im Hinweis, so kann keine Teilfolge eine Cauchyfolge sein, und damit auch keine Teilfolge konvergieren, da jede konvergente Folge eine Cauchyfolge ist (hier gilt sogar die Umkehrung, da \(C([0, 1])\) mit der uniformen Norm vollständig ist).
Beispiel für eine solche Folge wäre z.B. eine Funktion, die Null überall ist und dann an einer Stelle zur 1 hochgeht, und für jedes Folgenglied soll dies an einer anderen Stelle passieren.
Um Stetigkeit zu erfüllen, kann man z.B. wie ein Zacken hoch zur 1 gehen, formal also (\( h \) ist einfach nur eine Hilfsfunktion, die dir einen solchen Zacken auf dem Interval
\( [ a, b] \) gibt):
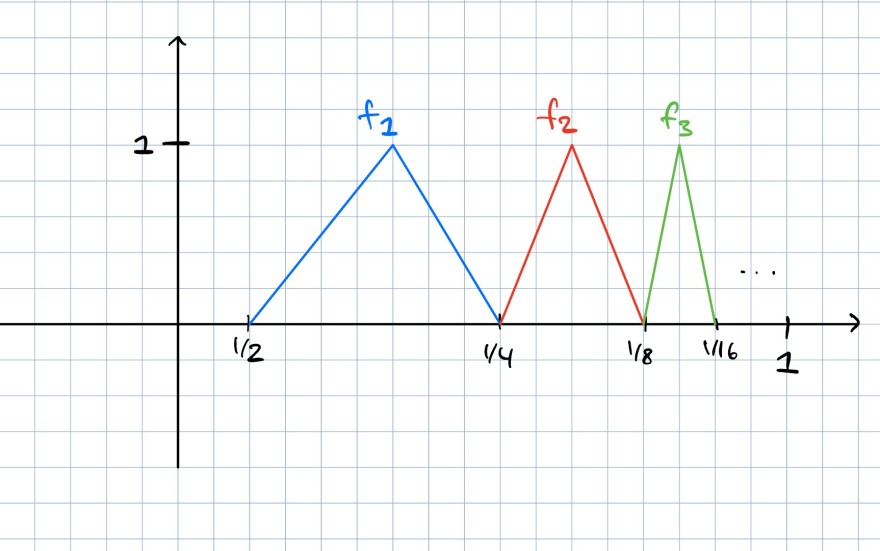
\(\begin{aligned} h _{ [ a, b] } ( x) &= \begin{cases} 2x / ( b - a) , & x \in [ a, ( b - a) / 2 ] \\ 1- 2( x - ( b - a) / 2 ) / ( b - a) , & x \in [ ( b - a) / 2 , b] \\ 0, & \text{sonst} \end{cases} \\[30pt] f _{ n} ( x) &= h _{ [ 2^{ -n}, 2^{ -( n + 1) }] } ( x) .\end{aligned}\)
Ein Bild sagt mehr als tausend Worte: