Aufgabe:
Text erkannt:
Mathematik HBF M O
FHR-Prüfung
Übungen
Aufgabe 7:
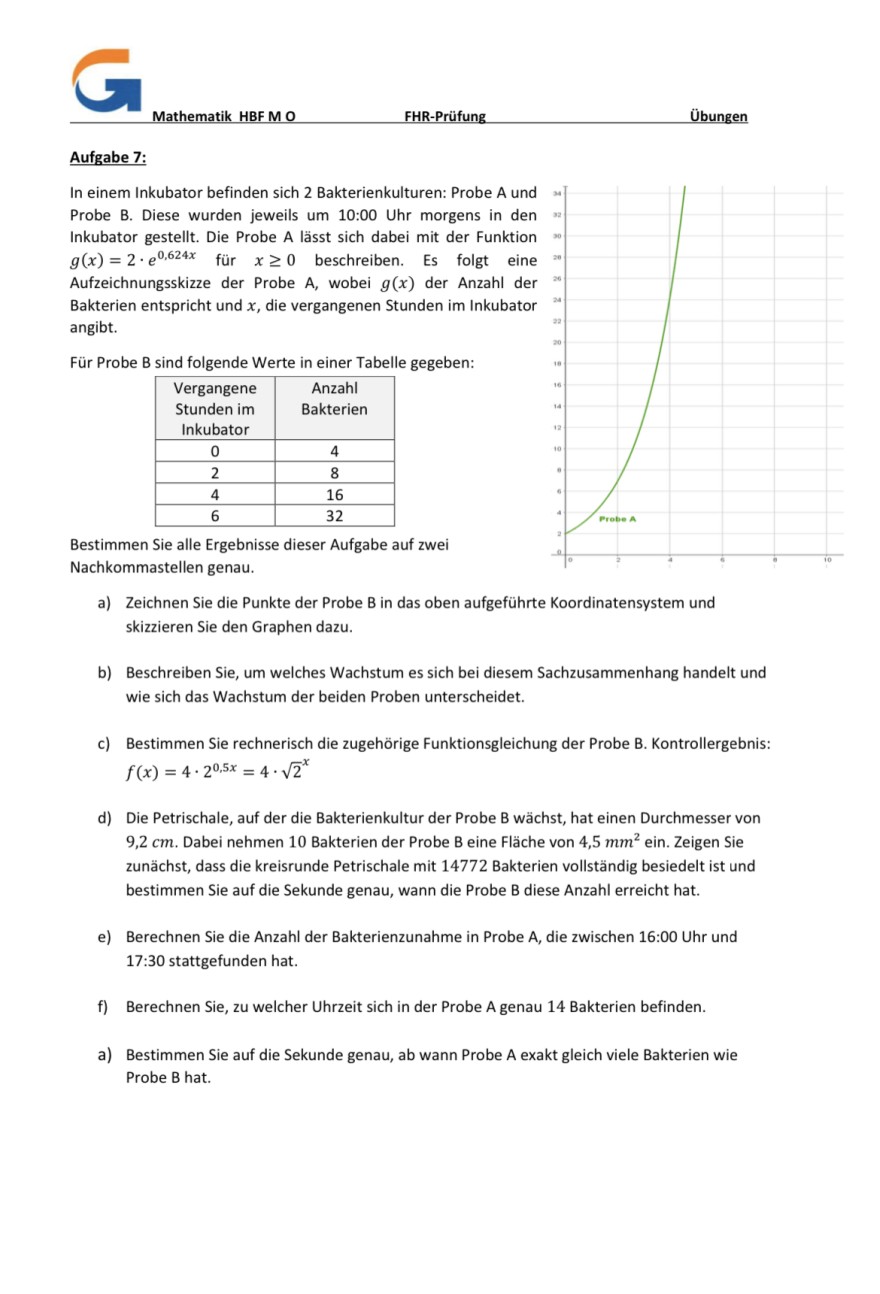
In einem Inkubator befinden sich 2 Bakterienkulturen: Probe \( A \) und Probe B. Diese wurden jeweils um 10:00 Uhr morgens in den Inkubator gestellt. Die Probe A lässt sich dabei mit der Funktion \( g(x)=2 \cdot e^{0,624 x} \) für \( x \geq 0 \) beschreiben. Es folgt eine Aufzeichnungsskizze der Probe A, wobei \( g(x) \) der Anzahl der Bakterien entspricht und \( x \), die vergangenen Stunden im Inkubator angibt.
Für Probe \( B \) sind folgende Werte in einer Tabelle gegeben:
\begin{tabular}{|c|c|}
\hline \( \begin{array}{c}\text { Vergangene } \\ \text { Stunden im } \\ \text { Inkubator }\end{array} \) & \( \begin{array}{c}\text { Anzahl } \\ \text { Bakterien }\end{array} \) \\
\hline 0 & 4 \\
\hline 2 & 8 \\
\hline 4 & 16 \\
\hline 6 & 32 \\
\hline
\end{tabular}
Bestimmen Sie alle Ergebnisse dieser Aufgabe auf zwei Nachkommastellen genau.
a) Zeichnen Sie die Punkte der Probe B in das oben aufgeführte Koordinatensystem und skizzieren Sie den Graphen dazu.
b) Beschreiben Sie, um welches Wachstum es sich bei diesem Sachzusammenhang handelt und wie sich das Wachstum der beiden Proben unterscheidet.
c) Bestimmen Sie rechnerisch die zugehörige Funktionsgleichung der Probe B. Kontrollergebnis:
\( f(x)=4 \cdot 2^{0,5 x}=4 \cdot \sqrt{2}^{x} \)
d) Die Petrischale, auf der die Bakterienkultur der Probe B wächst, hat einen Durchmesser von 9,2 cm. Dabei nehmen 10 Bakterien der Probe B eine Fläche von \( 4,5 \mathrm{~mm}^{2} \) ein. Zeigen Sie zunächst, dass die kreisrunde Petrischale mit 14772 Bakterien vollständig besiedelt ist und bestimmen Sie auf die Sekunde genau, wann die Probe B diese Anzahl erreicht hat.
e) Berechnen Sie die Anzahl der Bakterienzunahme in Probe A, die zwischen 16:00 Uhr und 17:30 stattgefunden hat.
f) Berechnen Sie, zu welcher Uhrzeit sich in der Probe A genau 14 Bakterien befinden.
a) Bestimmen Sie auf die Sekunde genau, ab wann Probe A exakt gleich viele Bakterien wie Probe \( B \) hat.
Problem/Ansatz:
Wie werden die Aufgaben gelöst?