Klassenarbeit Integralrechnung Schmuckstück Fläche mit Blattgold belegen

Question

Aufgabe:

…

Problem/Ansatz:

Wie löse ich diese Klassenarbeit?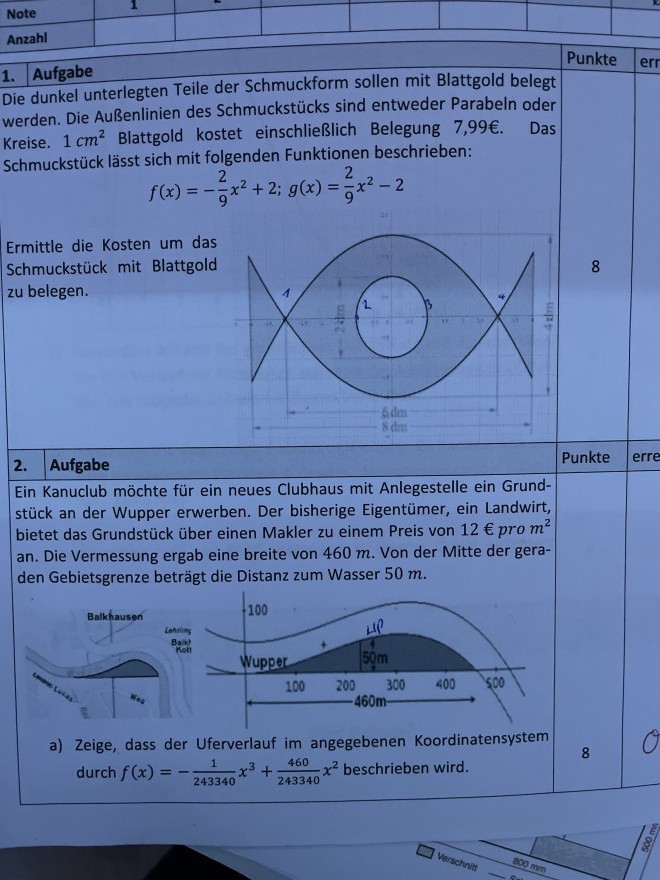

Text erkannt:

1. Aufgabe
Die dunkel unterlegten Teile der Schmuckform sollen mit Blattgold belegt werden. Die Außenlinien des Schmuckstücks sind entweder Parabeln oder Kreise. \( 1 \mathrm{~cm}^{2} \) Blattgold kostet einschließlich Belegung 7,99€. Das Schmuckstück lässt sich mit folgenden Funktionen beschrieben:
\( f(x)=-\frac{2}{9} x^{2}+2 ; g(x)=\frac{2}{9} x^{2}-2 \)
Ermittle die Kosten um das Schmuckstück mit Blattgold zu belegen.
2. Aufgabe
Ein Kanuclub möchte für ein neues Clubhaus mit Anlegestelle ein Grundstück an der Wupper erwerben. Der bisherige Eigentümer, ein Landwirt, bietet das Grundstück über einen Makler zu einem Preis von \( 12 € \) pro \( \mathrm{m}^{2} \) an. Die Vermessung ergab eine breite von \( 460 \mathrm{~m} \). Von der Mitte der geraden Gebietsgrenze beträgt die Distanz zum Wasser \( 50 \mathrm{~m} \).
a) Zeige, dass der Uferverlauf im angegebenen Koordinatensystem durch \( f(x)=-\frac{1}{243340} x^{3}+\frac{460}{243340} x^{2} \) beschrieben wird

Text erkannt:

b) Berechne die Größe des Grundstücks und ermittle den gesamten Kaufpreis, wenn der Makler eine Maklergebühr in Höhe von \( 3,48 \% \) veranschlagt.
3. Aufgabe
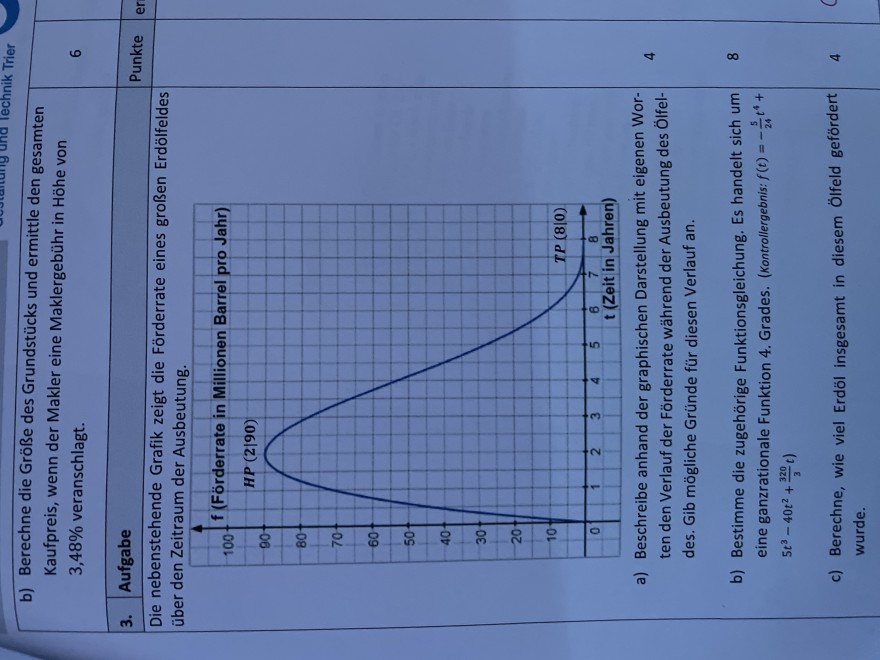
Die nebenstehende Grafik zeigt die Förderrate eines großen Erdölfeldes über den Zeitraum der Ausbeutung.
a) Beschreibe anhand der graphischen Darstellung mit eigenen Worten den Verlauf der Förderrate während der Ausbeutung des Ölfeldes. Gib mögliche Gründe für diesen Verlauf an.
b) Bestimme die zugehörige Funktionsgleichung. Es handelt sich um
8 eine ganzrationale Funktion 4. Grades. (Kontrollergebnis: \( f(t)=-\frac{5}{24} t^{4}+ \) \( \left.5 t^{3}-40 t^{2}+\frac{320}{3} t\right) \)
c) Berechne, wie viel Erdöl insgesamt in diesem Ölfeld gefördert wurde.

Answer 1

zu 1. Das ganze "Schmuckstück" geht wohl von -4 bis 4.

Die Fläche zwischen den Parabeln kannst du durch 3 Integrale

über die Differenz der Funktionen ausrechnen.

Von -4 bis zur 1. Schnittstelle , dann von der 1.

zur 2. und dann von der 2. bis 4.

Dann noch den Kreis abziehen und du hast die Fläche.

Gib mal deine Lösung bekannt, wir

korrigieren ggf.

Comments

Text erkannt:

is alles in dro
\( 3 \mathrm{Ban}\left\{\begin{array}{l}1,8 \mathrm{~cm} \\ 1,8 \mathrm{~cm}\end{array}\right] \times 2 \)
\( \begin{array}{l} 3 \cdot 1,8+3 \cdot 1,8+6,28 \quad 15,7 \\ \int \limits_{-3}^{3} x d x=\left[\frac{1}{3} \cdot\left(-\frac{2}{9}\right) \cdot 3^{3}+\frac{7}{7} \cdot 2\right. \\ \end{array} \)
人-Schrit
\( \left\{\int \limits_{-3}^{3} x d x=\left[\frac{1}{3} \cdot\left(-\frac{2}{9}\right) \cdot 3^{3}+\frac{7}{7} \cdot 2\right.\right. \)
\( \begin{array}{l} \left.\Rightarrow x=-\frac{2}{9} x^{2}+2=0 x \frac{2}{9} x^{2}-2\right) \int \limits_{-3}^{-3} \int^{3} x d x=24 d m \\ +\frac{2}{9} x^{2}+\frac{2}{9} x^{2}=2 z-2(-2) \\ \end{array} \)
endergebnis
\( \frac{\frac{4}{9} x^{2}=-4}{x^{2}=9} \quad 1: 4 \quad \text { 2.Schrit } \)
\( \begin{array}{l} 60 \mathrm{~cm} \\ \begin{array}{l} x^{2}=9 \\ x=3 \end{array} \quad 15 \\ \end{array} \)
\( -\frac{2}{9} x^{2}+2=\frac{2}{9} x^{2}-2 \quad \) Term umformen
\( -\frac{2}{9} x^{-}-\frac{2}{g} x^{2}=-2-2 \quad \) |rechnen 2sm
\( -\frac{4}{9} x^{2}=-4 \quad 1: 4 \)
\( x^{2}=9 \quad 1 \sqrt{1} \)
\( x_{1}=3 \quad x_{2}=-3 \)
\( F(x)=\frac{1}{3}-\frac{2}{9} x^{3}+\frac{1}{1} \cdot 2 x \)

Ich hoffe man kann erkennen aus dem Wirrwarr was ich versucht habe zu errechnen. Bitte wenn möglich mir den Richtigen Lösungsweg erklären falls der Ansatz falsch war. LG