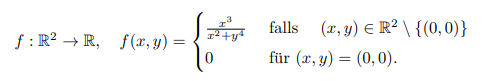
Text erkannt:
\( f: \mathbb{R}^{2} \rightarrow \mathbb{R}, \quad f(x, y)=\left\{\begin{array}{ll}\frac{x^{3}}{x^{2}+y^{4}} & \text { falls } \quad(x, y) \in \mathbb{R}^{2} \backslash\{(0,0)\} \\ 0 & \text { für }(x, y)=(0,0)\end{array}\right. \)
Bestimmen Sie die partiellen Ableitungen der Funktion und die Richtungsableitung in Richtung
v = (v1, v2)∈ R^2 ,v1 ungleich 0 im Nullpunkt. (Drucken Sie die Richtungsableitung allgemein durch die ¨
Komponenten v1, v2 von v aus.)
Text erkannt:
Sei
\( f: \mathbb{R}^{2} \rightarrow \mathbb{R}, \quad f(x, y)=\left\{\begin{array}{ll} \frac{x^{3}}{x^{2}+y^{4}} & \text { falls } \quad(x, y) \in \mathbb{R}^{2} \backslash\{(0,0)\} \\ 0 & \text { für }(x, y)=(0,0) . \end{array}\right. \)
Bestimmen Sie die partiellen Ableitungen der Funktion und die Richtungsableitung in Richtung \( \vec{v}=\left(v_{1}, v_{2}\right) \in \mathbb{R}^{2}, v_{1} \neq 0 \) im Nullpunkt. (Drücken Sie die Richtungsableitung allgemein durch die Komponenten \( v_{1}, v_{2} \) von \( \vec{v} \) aus.)
Problem/Ansatz:
Wie kann man diese aufgabe am besten lösen?