Aufgabe: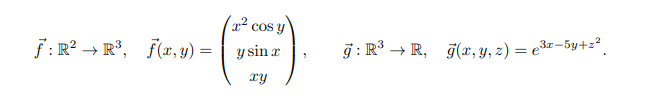
Text erkannt:
\( \vec{f}: \mathbb{R}^{2} \rightarrow \mathbb{R}^{3}, \quad \vec{f}(x, y)=\left(\begin{array}{c}x^{2} \cos y \\ y \sin x \\ x y\end{array}\right), \quad \vec{g}: \mathbb{R}^{3} \rightarrow \mathbb{R}, \quad \vec{g}(x, y, z)=e^{3 x-5 y+z^{2}} \).
Komposition g◦f ohne kettenregel bestimmen.
…
Problem/Ansatz:Bei der Partiellen ableitung kommt bei f eine 2x3 matrix und bei g eine 3x1 matrix raus.
Ich verstehe nicht ganz wie ich f in g einsetzen soll.