Aufgabe:
Text erkannt:
Exercise 2 (Change of variables, 5 points) Recall that if \( g: A \subseteq \mathbb{R} \rightarrow \mathbb{R} \) is an arbitrary function, its graph \( G_{g} \) is the subset of \( \mathbb{R} \times \mathbb{R} \) defined by the relation
\( G_{g}:=\{(x, g(x)): x \in A\} \)
Denote by \( E \) the bounded subset of \( \mathbb{R}_{+} \times \mathbb{R}_{+} \)delimited by the graph of the following functions: \( g_{1}(x)=1 / x \), \( g_{2}(x)=4 / x, g_{3}(x)=x / 4 \) and \( g_{4}(x)=4 x \).
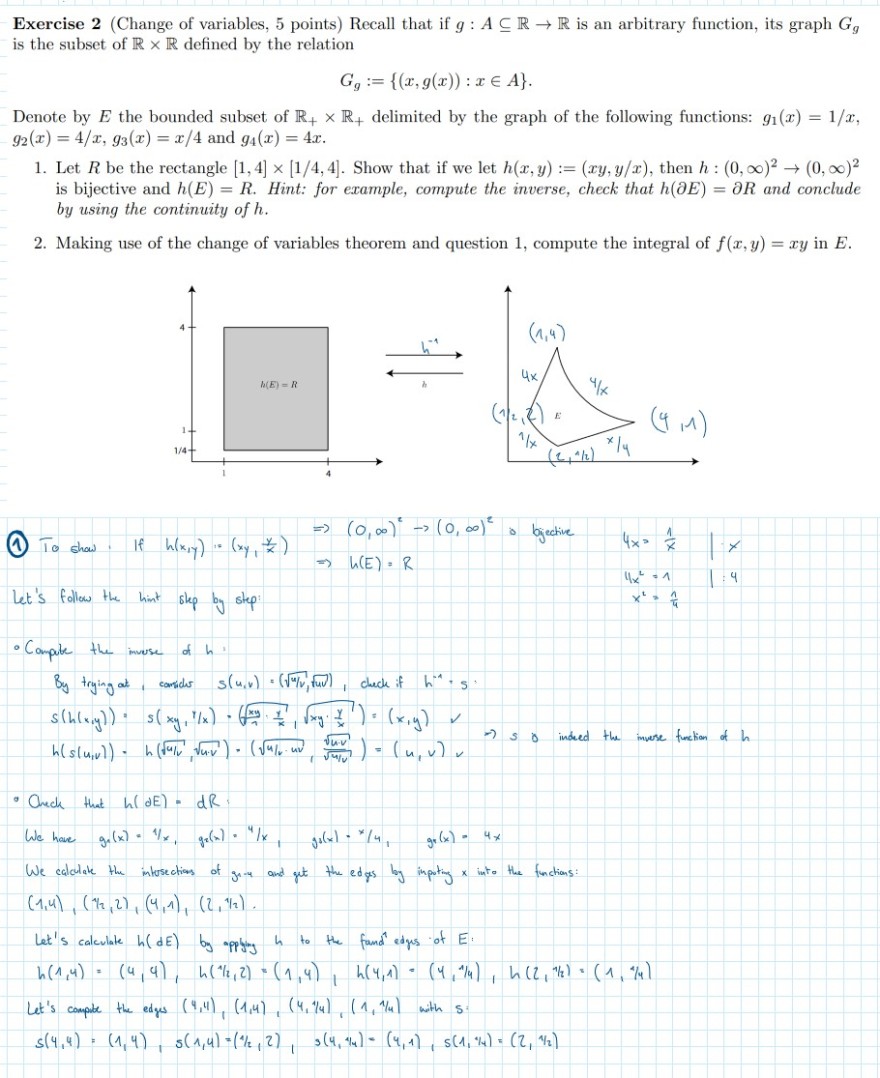
1. Let \( R \) be the rectangle \( [1,4] \times[1 / 4,4] \). Show that if we let \( h(x, y):=(x y, y / x) \), then \( h:(0, \infty)^{2} \rightarrow(0, \infty)^{2} \) is bijective and \( h(E)=R \). Hint: for example, compute the inverse, check that \( h(\partial E)=\partial R \) and conclude by using the continuity of \( h \).
2. Making use of the change of variables theorem and question 1, compute the integral of \( f(x, y)=x y \) in \( E \).
(1) To show. If \( h(x, y)=\left(x y, \frac{y}{x}\right) \)
\( \begin{array}{l} \Rightarrow(0, \infty)^{2} \rightarrow(0, \infty)^{2} \text { \& bjective } \\ \Rightarrow h(E)=R \end{array} \)
Let's follow the hint ske by step:
\( \begin{array}{l|l} 4 x=\frac{1}{x} & \mid x \\ 4 x^{2}=1 & \mid=4 \\ x^{2}=\frac{1}{4} & \end{array} \)
- Compie the imvese of \( h \)
By trying at, carrds \( s(u, v)=(\sqrt{u v}, t, \vec{u}) \), cleck if \( h^{-1}: s \)
\( \begin{array}{l} s(h(x, y))=s(x y, r / x) \cdot\left(\sqrt{\frac{x y}{1} \cdot \frac{y}{x}}, \sqrt{x y \cdot \frac{y}{x}}\right)=(x, y), v \Rightarrow s \text { o inbed the imese fucction of } h \\ h(s(u, v)) \cdot h(\sqrt{u / v}, \sqrt{u \cdot v}) \cdot\left(\sqrt{u / v \cdot u v}, \frac{\sqrt{u v}}{\sqrt{u / v}}\right)=(u, v), \end{array} \)
- Onck that \( h(d E)=d R \)
We have \( g_{1}(x)=1 / x, g_{2}(x) \cdot 4 / x, \quad g_{1}(x) \cdot x / 4, \quad g_{2}(x)=4 x \)
We ealculak the intosections of gre- and get the edys boy inpotigy \( x \) into the functian:
\( (1,4),(1 / 2,2),(4,1),(2,1 / 2) \)
Let's calculate \( h(d E) \) by appyer \( h \) to the fand ed edys of \( E \) :
\( h(1,4)=(4,4), h(1 / 2,2)=(1,4), h(4,1)=(4,1 / 4), h(2,1 / 2)=(1,1 / 4) \)
Let's compte the edys \( (4,4),(1,4),(4,1 / 4),(1,1 / 4) \) with 5 :
\( s(4,4)=(1,4), \quad s(1,4)=(1 / 2,2), \quad s(4,44)=(4,1), s(1,44)=(2,1 / 2) \)
Problem/Ansatz:
Anmerkung: Wir betrachten nur die Aufgabe 1. Ich muss zuerst h(dE) = dR zeigen. Nun habe ich wahrscheinlich nicht den gewünschten Weg genommen und habe stattdessen die Schnittpunkte/Ecken von E berechnet und darauf h angewendet und bekam somit die Eckpunkte von R. Vice versa habe ich diese Punkte in die berechnete Inverse Funktion s gesteckt und bekam die Eckpunkte von E. Habe ich damit gezeigt, dass dE = dR ist?