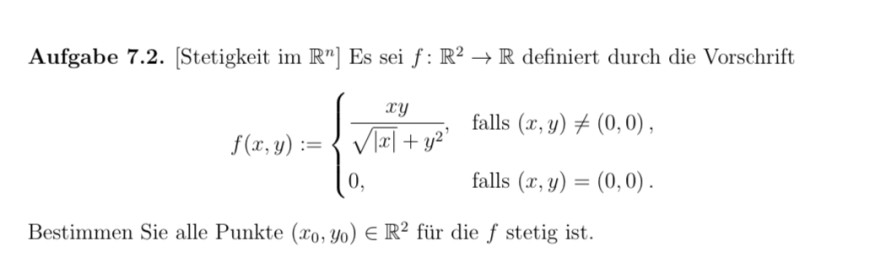
Text erkannt:
Aufgabe 7.2. [Stetigkeit im \( \left.\mathbb{R}^{n}\right] \) Es sei \( f: \mathbb{R}^{2} \rightarrow \mathbb{R} \) definiert durch die Vorschrift
\( f(x, y):=\left\{\begin{array}{ll} \frac{x y}{\sqrt{|x|}+y^{2}}, & \text { falls }(x, y) \neq(0,0), \\ 0, & \text { falls }(x, y)=(0,0) . \end{array}\right. \)
Bestimmen Sie alle Punkte \( \left(x_{0}, y_{0}\right) \in \mathbb{R}^{2} \) für die \( f \) stetig ist.
Aufgabe:
Problem/Ansatz
Ich habe limes berechnet und kam 1/2 zwei was unlogisch aussieht.
Kann mir eine bitte den Losungsweg ausführlich beschreiben und die Aufgabe Losen, somit ich sie mit meiner Losung vergleichen kann!
Vielen Dank im Voraus