Hallo,
\( \begin{array}{l}f(x)=(2 x+2) \cdot e^{-0,5 x} \\ f^{\prime}(x)=(1-x) \cdot e^{-0,5 x} \\ f^{\prime \prime}(x)=\frac{(x-3)}{2} \cdot e^{-0,5 x}\end{array} \)
Nullstellen: Setze f(x) = 0 und löse nach x auf, wende den Satz vom Nullprodukt an
Extrema: Setze f'(x) = 0, löse nach x auf, wende auch hierbei den Satz vom Nullprodukt an.
Setze dein Ergebnis in f''(x) ein, um Hoch- oder Tiefpunkt zu bestimmen. Zur Berechnung der y-Koordinate setzt du dein Ergebnis in f(x) ein.
Wendepunkte: Setze f''(x) = 0 ...
Grenzwertverhalten: Plotte die Funktion und betrachte den Verlauf des Graphen nach \(\pm \infty\)
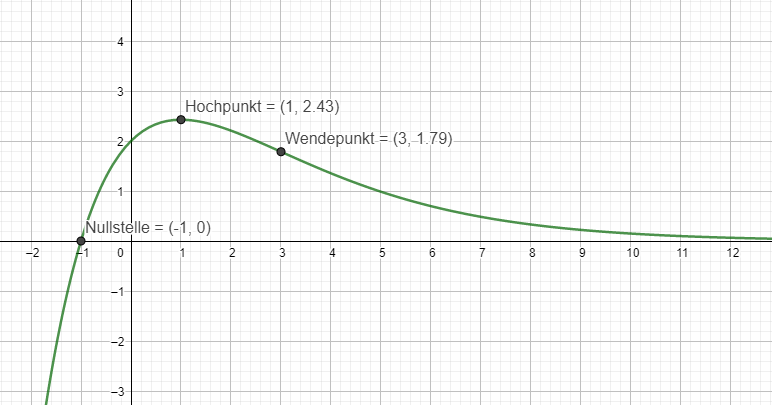
So gehst du auch bei der 2. Aufgabe vor.
\(f(x)=(1-x)\cdot e^{2-x}\\ f'(x)=(x-2)\cdot e^{2-x}\\ f''(x)=(3-x)\cdot e^{2-x}\)
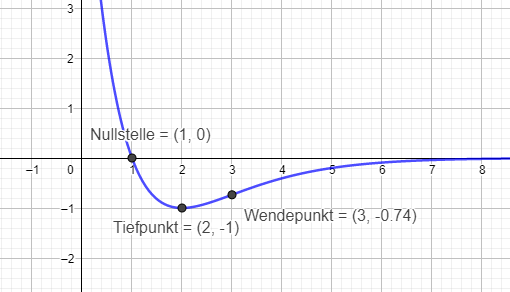
Gruß, Silvia