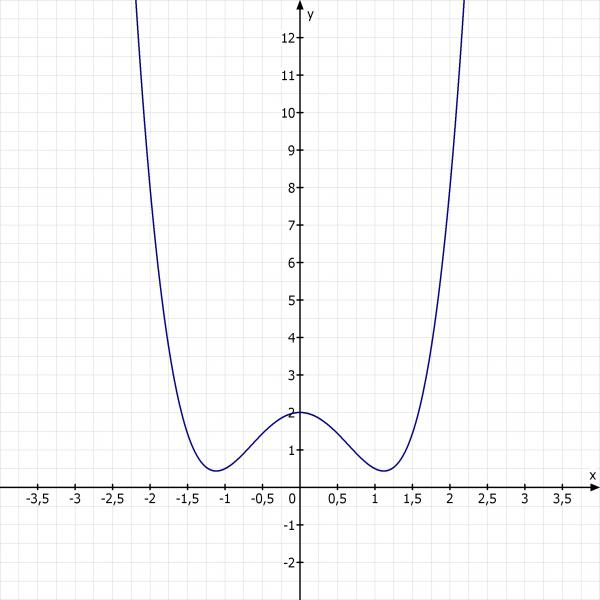
f(x) = x^4 - 2.5x^2 + 2
f'(x) = 4·x^3 - 5·x
f''(x) = 12·x^2 - 5
Achsensymmetrisch zur y-Achse. Daher kann man die Kurvendiskussion auf den Positiven Bereich beschränken.
Y-Achsanabschnitt bei f(0)
f(0) = 2
Nullstellen f(x) = 0
x^4 - 2.5x^2 + 2 = 0
z^2 - 2.5z + 2 = 0
Keine Nullstellen
Extremstellen f'(x) = 0
4·x^3 - 5·x = x·(4·x^2 - 5) = 0
x1 = 0
4·x^2 - 5 = 0
x2 = √5/2
f(0) = 2 --> HP(0, 2)
f(√5/2) = 7/16 --> TP(√5/2, 7/16)
Wendestellen f''(x) = 0
12·x^2 - 5 = 0
x = √(5/12) = √15/6
f(√15/6) = 163/144 --> WP(√15/6, 163/144)
Skizze