Ableitung von Sinus und Cosinus (partielle Ableitung)

Question

Aufgabe:

Wir betrachten die Funktionen \( f: \mathbb{R}^{2} \rightarrow \mathbb{R}, f(x, y)=\cos (x-y)-\sin ^{2}(x) \) und \( g: \mathbb{R}^{2} \rightarrow \mathbb{R}, g(x, y)=x^{3}-3 x y^{2} \).

(a) Bestimmen Sie die Gradienten von \( f \) und \( g \).

Problem/Ansatz:

Ich bin mir unsicher, ob meine Rechnung richtig ist. CGPT gibt mir (siehe Bild) diese Ergebnisse aus. Ich komme aber auf ein anderes Ergebnis, nämlich:

fx = -sin(x-y)-2sin(x)cos(x)

fxx = -cos(x-y)- (hier bin ich mir nicht sicher, wie ich 2sin(x)cos(x) ableite)

fy = sin(x,y)

fyy = cos(x,y) -> Hier verstehe ich nicht, wieso ein negatives Vorzeichen vorgeschlagen wird. Die Ableitung von Sinus ist doch ein positiver Cosinus?

fxy = -cos(x-y)

fyx = cos(x-y)

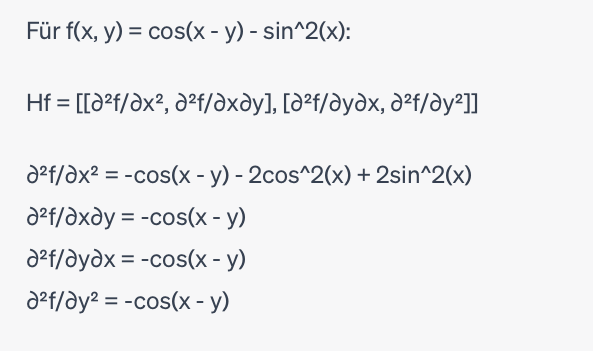
Ich danke im Voraus! :) 

Answer 1

(hier bin ich mir nicht sicher, wie ich 2sin(x)cos(x) ableite)

Produktregel und Faktorregel:

2*(cosx*cosx-sinx*sinx) = 2*(cos^2x -sin^2x)

cos(x-y) = cos(x)cos(y)+sin(x)sin(y)