Quadratische Form // Ellipse

Question

Aufgabe:

Ellipsen können als diejenigen Punkte \( \begin{pmatrix} x\\y \end{pmatrix} \)∈ R² beschrieben werden, für die die Summe der Abstände zu zwei fest gewählten Punkten P₁, P₂ konstant ist. Ein Beispiel wäre E: {\( \begin{pmatrix} x\\y \end{pmatrix} \)∈ R² Ι ΙΙ\( \begin{pmatrix} -3\\0 \end{pmatrix} \)-\( \begin{pmatrix} x\\y \end{pmatrix} \)ΙΙ + ΙΙ\( \begin{pmatrix} 3\\0 \end{pmatrix} \)-\( \begin{pmatrix} x\\y \end{pmatrix} \)ΙΙ = 10}

Geben Sie eine quadratische Form q : R² → R an, so dass E= {\( \begin{pmatrix} x\\y \end{pmatrix} \)∈ R² Ι q\( \begin{pmatrix} x\\y \end{pmatrix} \)=1}

Ich bin etwas überfordert und weiß nicht wie ich anzufangen habe. Was ich weiß ist das q\( \begin{pmatrix} x\\y \end{pmatrix} \) : ax² + by² diese Form annehmen sollte. Aber wie bestimme ich das a bzw. b?

Comments

Hallo

statt "Die Aufgabe verlangt von mir" poste die Originalaufgabe! so ist unklar, etwa soll der Abstand von P1 und P2 1 sein? wo liegen P1 und P2 usw.

lul

---

Danke das du mich darauf aufmerksam gemacht hast, habe sie nun bearbeitet.

Answer 1

Hallo

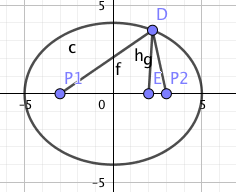
sei D ein allgemeiner Punkt auf der Ellipse, dann kannst du mit Pythagoras die Abstände zu P1,P2 bestimmen, addieren und hast eine form der Ellipsengleichung.

du kannst auch direkt die Achsen der Ellipse ausrechnen, da der Punkt (0,4) darauf liegen muss und den Punkt auf der x-Achse kann man auch ohne Pythagoras ausrechnen. damit hast du die 2 Achsen,  a,b, sind die Halbachsen, wenn man  die Ellipsengleichung als x^2/a^2+y^2/b^2=1 schreibt, (zur Kontrolle a=5,b=4

Gruß lul

Comments

Danke dir für die Mühe als auch für die schnelle Antwort. Ich habe allerdings eine Frage:

Ich bin jetzt leider nicht der absolute Kenner auf diesem Gebiet aber ich dachte immer wenn die Länge 1 sein soll, dass dann damit gemeint ist das die Hauptachse 1 lang ist. Bei dir ist sie aber 10 lang. Wie kommt man darauf?

---

Hallo

da steht q/x,y)=1 das hab ich aufgeschrieben, darüber steht der Betrag der Abstandssumme ist 10

||(−3,0)-\( \begin{pmatrix} x\\y \end{pmatrix} \)ΙΙ + ΙΙ\( \begin{pmatrix} 3\\0 \end{pmatrix} \)-\( \begin{pmatrix} x\\y \end{pmatrix} \)ΙΙ = 10}

lul