Aufgabe:
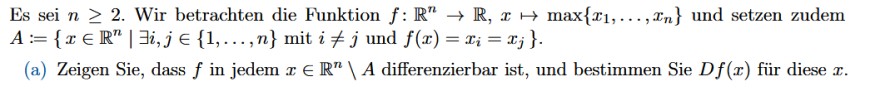
Text erkannt:
Es sei \( n \geq 2 \). Wir betrachten die Funktion \( f: \mathbb{R}^{n} \rightarrow \mathbb{R}, x \mapsto \max \left\{x_{1}, \ldots, x_{n}\right\} \) und setzen zudem \( A:=\left\{x \in \mathbb{R}^{n} \mid \exists i, j \in\{1, \ldots, n\}\right. \) mit \( i \neq j \) und \( \left.f(x)=x_{i}=x_{j}\right\} \).
(a) Zeigen Sie, dass \( f \) in jedem \( x \in \mathbb{R}^{n} \backslash A \) differenzierbar ist, und bestimmen Sie \( D f(x) \) für diese \( x \).
Problem/Ansatz:
Ich habe es über die Defintion versucht aber irgendwie haut das nicht so hin. Würde mich über tipps freuen