Aufgabe:
Zeigen Sie, dass
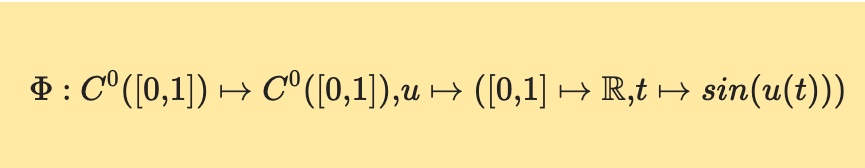
Text erkannt:
\( \Phi: C^{0}([0,1]) \mapsto C^{0}([0,1]), u \mapsto([0,1] \mapsto \mathbb{R}, t \mapsto \sin (u(t))) \)
differenzierbar ist, und bestimmen Sie DΦ.
Problem/Ansatz:
Das Hauptproblem besteht darin, die Stetigkeit von $D\Phi$ zu zeigen (wie? und warum ist die Stetigkeit relevant). Als Voraussetzung für die Stetigkeit können wir die Stetigkeit der Funktion $u$ annehmen. Um die Stetigkeit von $\Phi$ zu beweisen, können wir die Kettenregel verwenden, da $\Phi$ eine Verkettungsfunktion ist.
Eine weitere Überlegung ist die Konvergenz der Funktion $u(t)$, da sie den Sinus einer Funktion verwendet. Wir können darauf hinweisen, dass für $t$ im Intervall $[0,1]$ der Sinus eine wohldefinierte Funktion ist und somit die Konvergenz von $u(t)$ sichergestellt ist. Wie geht es dann weiter ?
oder gibt es einen eleganteren Weg?