Exponentialfunktion: f(x) = (x - 2)^2·e^x

Question

Aufgabe:

Woran erkennt man, dass die Funktion f(x) = (x-2)hoch 2 mal e hoch 2 zu diesem Graphen gehört.

Comments

Vom Duplikat:

Titel: Aufstellen von E-Funktione

Stichworte: e-funktion,eulersche,funktion

Aufgabe:

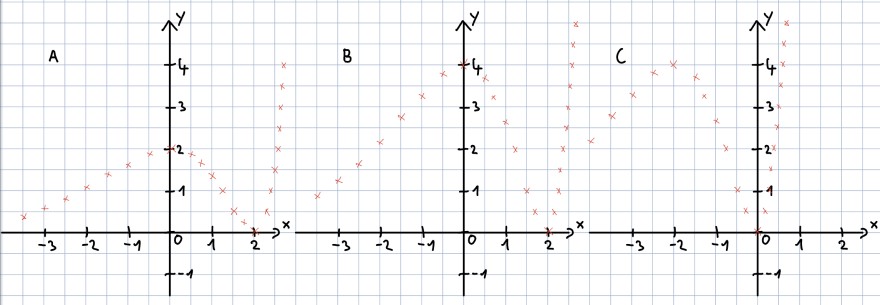
Einer der Graphen gehört zur Funktion f mit f(x) = (x - 2)hoch 2 mal e hoch x.
a) Ordnen Sie der Funktion den zugehörigen Graphen zu und begründen Sie die Wahl.
b) Geben Sie die Funktionsterme zu den beiden anderen Graphen an.

Problem/Ansatz:

Bräuchte bitte bei der b) Hilfe/einen Ansatz.

Lösung zur Überprüfung wäre auch sehr hilfreich.

Die Kreuze stellen die Graphen dar.

---

Was hast du genau nicht verstanden gehabt?

Answer 1

Vielleicht hilft dir folgende Skizze

~plot~ (x-2)^2*e^x;1/2*(x-2)^2*e^x;(x)^2*e^(x+2);[[-8|4|-2|6]] ~plot~

Comments

Vielen Dank, wie kann ich bei der B rechnerisch darauf kommen?

---

Schau wie sich die Graphen von dem blauen unterscheiden.

Der rote ist nur mit dem Faktor 1/2 in y-Richtung gestaucht.

Der grüne ist nur um 2 Einheiten nach links verschoben.

Also brauchst du den original Funktionsterm nur verändern. Schau also mal wie ich die Funktion verändert habe.

Rechnen muss man dort eigentlich nichts.

Answer 2

Die Funktion \(g(x) = (x-2)^2\) ist eine um 2 nach rechts verschobene Normalparabel.

Die Funktion \(h(x) = \mathrm{e}^x\) geht gegen 0 für \(x\to \infty\) und gegen \(\infty\) für \(x\to \infty\)

Das Produkt verhält sich wie \(g\) in einer Umgebung, die eine Nullstelle von \(g\) hat. Ansonsten verhält es sich abgesehen vom Vorzeichen wie \(h\) weil Exponentialfunktionen für (\x\to \pm \infty\) gegenüber jeder Potenzfunktion durchsetzen.