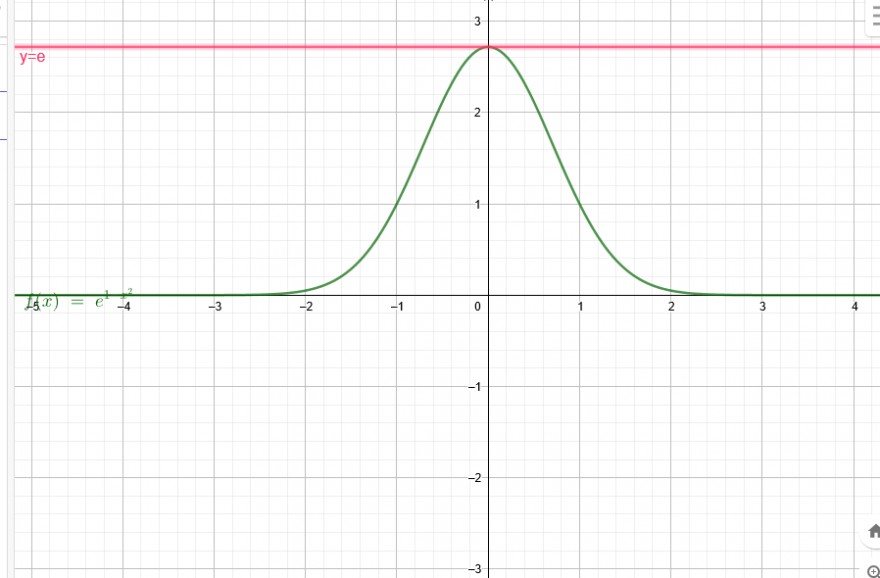
f(x)= \( e^{1-x^2} \)
f´(x)=-2x* \( e^{1-x^2} \)
f´´(x)=-2* \( e^{1-x^2} \)+(-2x)(-2x)* \( e^{1-x^2} \)=\( e^{1-x^2} \)*(4x^2-2)
f´´´(x)=...
Extremwert
f´(x)=0
-2x* \( e^{1-x^2} \)= 0
-2x=0 x=0 f(0)= e
\( e^{1-x^2} \) kann nicht Null werden.
Art des Extremwertes
f´´(0)=\( e^{1} \)*(4*0-2)=e*(-2)=-2e <0→Maximum