Ich habe eine recht spezielle Frage. Nämlich verstehe ich nicht genau, wie man eine Funktion richtig umstellt, um die Regeln von de l’Hospital anwenden zu dürfen. Dabei meine ich primär erstmal Funktionen, wo minus gerechnet wird, solche Beispiele habe ich schon oft gesehen und gefühlt wird da jedes mal anders umgestellt. Was ich meine:
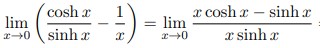
Text erkannt:
\( \lim \limits_{x \rightarrow 0}\left(\frac{\cosh x}{\sinh x}-\frac{1}{x}\right)=\lim \limits_{x \rightarrow 0} \frac{x \cosh x-\sinh x}{x \sinh x} \)
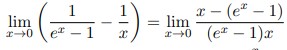
Text erkannt:
\( \lim \limits_{x \rightarrow 0}\left(\frac{1}{e^{x}-1}-\frac{1}{x}\right)=\lim \limits_{x \rightarrow 0} \frac{x-\left(e^{x}-1\right)}{\left(e^{x}-1\right) x} \)
Ich könnte noch viele weitere Beispiele beifügen, aber ich hoffe es ist klar was ich meine. Die einzige Gemeinsamkeit die ich immer sehe ist das im Zähler minus gerechnet wird und unten immer beide Nenner mal genommen werden, aber was genau soll im Zähler von was abgezogen werden? Kann da jemand Licht ins Dunkeln bringen?