Bestimmen Sie den zu f gehörigen Funktionsterm.

Question

Aufgabe:

Der Graph einer ganzrationalen Funktion dritten Grades \( f(x) \) hat in dem Punkt \( \left(x_{m}=2, y_{m}=16\right) \) ein Minimum. Außerdem ist dort die zweite Ableitung vom Wert 12 und die dritte Ableitung gleich 6.

a) Bestimmen Sie den zu \( f \) gehörigen Funktionsterm.

b) Warum führt der Ansatz

\( \begin{aligned} f(x)= & f(2)+f^{\prime}(2) \cdot(x-2) \\ & +\frac{1}{2} f^{\prime \prime}(2) \cdot(x-2)^{2} \\ & +\frac{1}{6} f^{\prime \prime \prime}(2) \cdot(x-2)^{3} \end{aligned} \)

zur selben Funktion?

Problem/Ansatz:

Wie muss man vorgehen? Kann mir jemand helfen?

Danke ;)

Answer 1

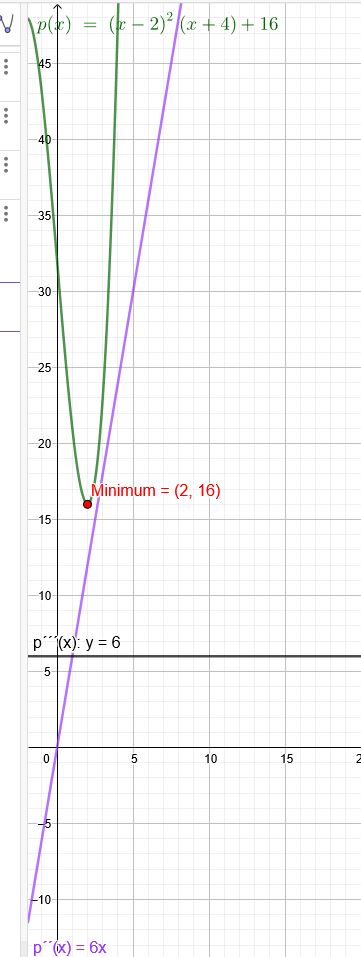
Der Graph einer ganzrationalen Funktion dritten Grades \( f(x) \) hat in dem Punkt \( P(2| 16) \) ein Minimum. Außerdem ist dort die zweite Ableitung vom Wert 12 und die dritte Ableitung gleich 6.

Ich verschiebe den Graph um 16 Einheiten nach unten :\( P´(2| 0) \) doppelte Nullstelle

\(p(x)=a*[(x-2)^2*(x-N)]\)

zweite Ableitung vom Wert 12:

\(p´(x)=a*[(2x-4)*(x-N)+(x-2)^2]\)

\(p´´(x)=a*[2x-2N+2x-4+2x-4=6x-2N-8]\)

\(p´´(2)=a*[6*2-2N-8]=a*[4-2N]=12\)    →  \(a=\frac{6}{2-N}\)

die dritte Ableitung gleich 6.

\(p´´´(x)=a*[6]\)

\(p´´´(2)=a*[6]=6\)→\(a=1\)     \(1=\frac{6}{2-N}\)  \(N=-4\)

\(p(x)=(x-2)^2*(x+4)\)

um 16 Einheiten nach oben:

\(f(x)=(x-2)^2*(x+4)+16\)

Answer 2

zu a) Betrachte die Bestimmung des Funktionsterms als Steckbriefaufgabe: Notiere die linearen Gleichungen, die sich aus den vier Bedingungen ergeben und löse das so entstehende lineare Gleichungssystem.

zu b) Der gegebene Ansatz entspricht der Taylorreihenentwicklung der Funktion \(f\) an der Stelle \(x=2\). Er besteht nur aus den vier angegebenen Gliedern, da alle weiteren Ableitungen \(0\) sind. Ob das als antwort gesucht ist, weiß ich nicht.