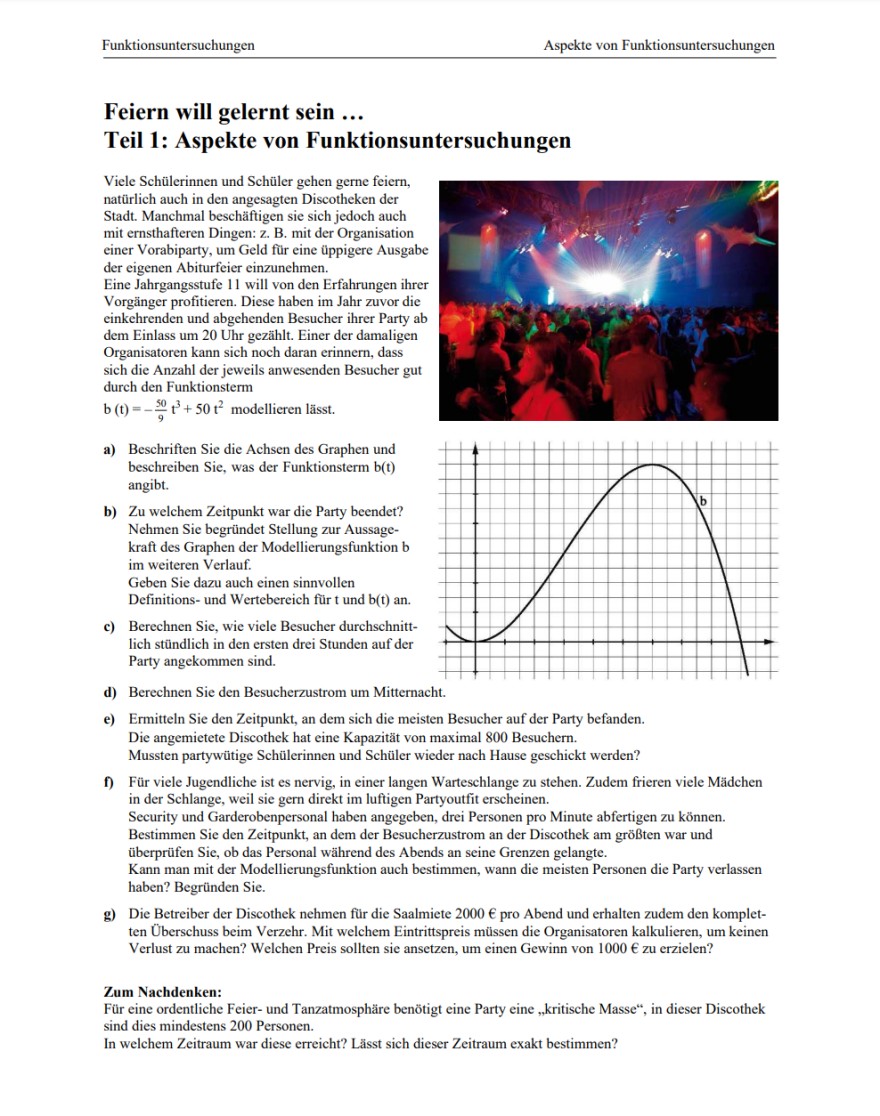
Aufgabe:
Problem/Ansatz:
Bei g)
Um den Eintrittspreis zu bestimmen, mit dem die Organisatoren keinen Verlust machen, müssen sie die Gesamtkosten decken, einschließlich der Saalmiete von 2000 € pro Abend. Da sie keinen Verlust machen möchten, muss der Eintrittspreis mindestens die Gesamtkosten abdecken.
Um den Eintrittspreis zu berechnen, nehmen wir an, dass die Gesamtkosten aus der Saalmiete und dem kompletten Überschuss beim Verzehr bestehen. Der Überschuss beim Verzehr hängt von der Anzahl der Besucher und dem Eintrittspreis ab.
Sei x die Anzahl der Besucher und p der Eintrittspreis. Der Überschuss beim Verzehr ergibt sich dann aus dem Produkt von x und p. Da die Organisatoren keinen Verlust machen möchten, muss der Eintrittspreis mindestens die Saalmiete abdecken, also:
p * x >= 2000
Um den Eintrittspreis zu berechnen, setzen wir die maximale Anzahl von Besuchern (800) ein:
p * 800 >= 2000
800p >= 2000
p >= 2000 / 800
p >= 2.5
Der Eintrittspreis sollte also mindestens 2,50 € betragen, um keinen Verlust zu machen.
Um einen Gewinn von 1000 € zu erzielen, müssen die Organisatoren neben den Gesamtkosten auch einen Gewinn von 1000 € erzielen. Der Eintrittspreis kann wie folgt berechnet werden:
p * x = 2000 + 1000
p * x = 3000
Wenn wir die maximale Anzahl von Besuchern (800) einsetzen, erhalten wir:
800p = 3000
p = 3000 / 800
p ≈ 3.75
Die Organisatoren sollten also einen Eintrittspreis von etwa 3,75 € festlegen, um einen Gewinn von 1000 € zu erzielen.
soweit richtig?