Bestimmen Sie jeweils das Taylor-Polynom dritter Ordnung um den gegebenen Entwicklungspunkt

Question

Ich bringe mir alles selbst bei und benötige Hilfe, damit ich verstehe, wie ich solche Aufgabentypen lösen kann. Vielen Dank für eure Hilfe.

Aufgabe:

Bestimmen Sie jeweils das Taylor-Polynom dritter Ordnung um den gegebenen
Entwicklungspunkt x₀ von f(x) und g(x)

Problem/Ansatz:

Text erkannt:

\( f(x)=\ln \left(\frac{1+e^{x}}{2}\right), \quad x_{0}=0 \)

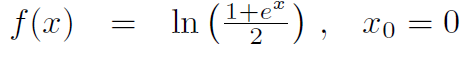
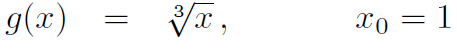
Text erkannt:

\( g(x)=\sqrt[3]{x}, \quad x_{0}=1 \)

Answer 1

1. Formel raussuchen.
2. In Formel einsetzen.
   

Welcher Teil bereitet dir Schwierigkeiten? Fall zweiterer, welchen Teil der Formel hast du nicht verstanden?

Comments

Ich habe das raus, stimmt das?

g(x) = 1 + 1/3 x - 1/9x^2 + 5/81 x^3

f(x) = 1/2 x + 1/8 x^2

Ich habe nämlich kein Gefühl dafür, ob mein Endergbenis korrekt ist. Vielen Dank für die Hilfe.

---

f(x) = 1/2 x + 1/8 x²

Ja, außer dass das nicht f(x) ist, sondern eben das Taylorpolynom dritter Ordnung von f.

g(x) = 1 + 1/3 x - 1/9x² + 5/81 x³

Nein.

---

Text erkannt:

\( \begin{array}{l} g^{(x)}=\sqrt[3]{x}=x^{\frac{3}{3}} \times x_{0}=1 \\ g^{\prime}(x)=\frac{1}{3} x^{\frac{1}{3}-1}=\frac{1}{3 x^{2 / 3}}=\frac{2}{\theta^{5 / 3}} \\ v^{\prime \prime}(x)=\frac{\left(-\frac{2}{3}\right) x^{-\frac{2}{3}-1}}{3}=\frac{2\left(-\frac{5}{3}\right) x^{-\frac{5}{3}-1}}{v}=\frac{10}{27 x^{8 / 3}} \end{array} \)
Wir echalken an der Stelle \( x_{0}=1 \) die Worte
\( \begin{aligned} g(1) & =1 \\ g^{\prime}(1) & =\frac{1}{3} \\ g^{\prime \prime}(1) & =-\frac{2}{3} \\ g^{\prime \prime}(1) & =\frac{10}{22} \\ T_{3}(x, 1) & =g(1)^{\prime}+g^{\prime}(1) \cdot x+g^{\prime \prime}(1) \cdot \frac{x^{2}}{2 !}+g^{\prime \prime \prime}(1) \frac{x^{3}}{3} \\ & =1+\frac{1}{3} x+\frac{2}{3} \cdot \frac{x^{2}}{2}+\frac{10}{22} \frac{x^{3}}{6}= \\ & =1+\frac{1}{3} x-\frac{1}{3} x^{3}+\frac{5}{81} \cdot x^{3} \end{aligned} \)

Wie lautet denn das richtige Ergebnis bei g(x)?

---

Das richtige Ergebnis lautet

        \(g(x_0) + g'(x_0)\cdot (x-x_0) + \frac{g''(x_0)}{2!}\cdot (x-x_0)^2 + \frac{g'''(x_0)}{3!}\cdot (x-x_0)^3\)

Der Entwicklungspunkt wirkt sich nicht nur darauf aus, wo die Ableitung berechnet wird, sondern auch darauf, was potenziert wird.

---

40/81 + 8/27x - 8/27x^2 +5/81 x^3

Vielen Dank für den Tipp. Stimmt die Rechnung jetzt so?

---

Ich habe es jetzt. Danke nochmal für alles.

Answer 2

40/81 + 8/27x - 8/27x2 +5/81 x3
stimmt das jetzt so?

Ich habe fast das gleiche heraus

T3(x) = 5/81·x^3 - 8/27·x^2 + 20/27·x + 40/81

Prüfe dein Ergebnis.. Übrigens brauchst du normal das Polynom nicht ausmultiplizieren. Ein Ergebnis der Form

T3(x) = 5/81·(x - 1)^3 - 1/9·(x - 1)^2 + 1/3·(x - 1) + 1

sollte normalerweise völlig ausreichend sein.

Comments

Tausend Dank für deine Zeit und Hilfe.