Aufgabe:

Text erkannt:
Es sei
\( p: \mathbb{C} \rightarrow \mathbb{C}, \quad z \mapsto \sum \limits_{k=0}^{n} a_{k} z^{k} \)
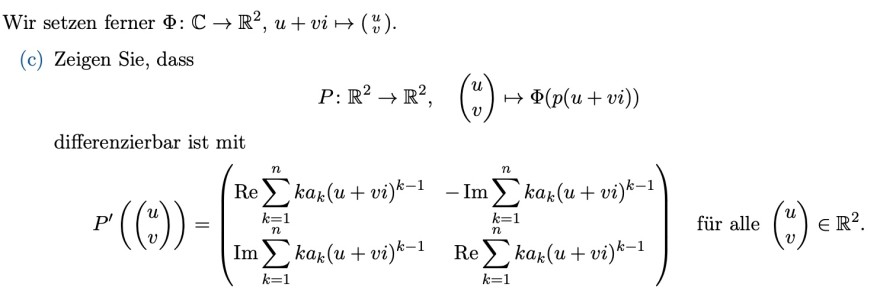
Text erkannt:
Wir setzen ferner \( \Phi: \mathbb{C} \rightarrow \mathbb{R}^{2}, u+v i \mapsto\left(\begin{array}{l}u \\ v\end{array}\right) \)
(c) Zeigen Sie, dass
\( P: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}, \quad\left(\begin{array}{l} u \\ v \end{array}\right) \mapsto \Phi(p(u+v i)) \)
differenzierbar ist mit
\( P^{\prime}\left(\left(\begin{array}{l} u \\ v \end{array}\right)\right)=\left(\begin{array}{cc} \operatorname{Re} \sum \limits_{k=1}^{n} k a_{k}(u+v i)^{k-1} & -\operatorname{Im} \sum \limits_{k=1}^{n} k a_{k}(u+v i)^{k-1} \\ \operatorname{Im} \sum \limits_{k=1}^{n} k a_{k}(u+v i)^{k-1} & \operatorname{Re} \sum \limits_{k=1}^{n} k a_{k}(u+v i)^{k-1} \end{array}\right) \quad \text { für alle }\left(\begin{array}{l} u \\ v \end{array}\right) \in \mathbb{R}^{2} \)
Problem/Ansatz:
Wir könnten die Komponentenfunktionen von P betrachten und zeigen, dass sie differenzierbar sind. Dann die partiellen Ableitungen der Komponentenfunktionen berechnen nach den Variablen u und v. Überprüfen, ob die partiellen Ableitungen stetig sind. Aber man soll es mit der allgemeinen Definition einer linearen Abbildung zeigen, und das kriegen wir nicht hin für Real-und Imaginärteil