Komplexes Polynom. Zu bestimmen sind alle komplexen Lösungen.
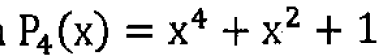
Text erkannt:
\( P_{4}(x)=x^{4}+x^{2}+1 \)
Ich würde hier substituieren mit z= x2 sodass ich erhalte:
P(z)= z2 +z +1
dann mit der PQ-Formel und radizieren.
Als Lösungen des Radizieren erhalte ich:
w0= \( \frac{\sqrt{3}}{2} \)
w1= -1
\( \frac{a}{b} \)
Text erkannt:
\( P_{4}(x)=x^{4}+x^{2}+1 \)
Mit dem Rest der PQ-Formel zusammengefasst erhalte ich als endgültige Ergebnisse:
z11= \( \frac{-1}{2} \) + \( \frac{\sqrt{3}}{2} \)
z12= \( \frac{-1}{2} \) - 1
z21= \( \frac{-1}{2} \) - \( \frac{\sqrt{3}}{2} \)
z22= \( \frac{-1}{2} \) + 1
Sind diese Ergebnisse richtig bzw. die Vorgehensweise? Denn ich habe am Ende nicht mehr rücksubstituiert, sofern dies nötig und möglich ist, aber wie weiß ich nicht.