Ich habe den zweiten Teil der Frage (Ermitteln...) gar nicht verstanden, ...
unumgänglich ist ein räumliche Vorstellung dessen, um das es hier geht!
Mal angenommen, die Gerade \(h\) sei:$$h: \quad \vec{x}(t) = \begin{pmatrix}3\\ 2\\ 4\end{pmatrix} + t\begin{pmatrix}-1\\ 2\\ 2\end{pmatrix}$$und die Ebene \(E\) ist die aus Deiner Aufgabenstellung \(x+y+z=1\). Ich habe Dir das in Geoknecht3D eingegeben:
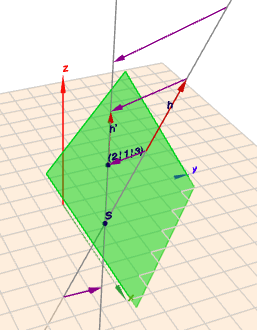
(klick auf das Bild, dann öffnet sich Geoknecht3D und Du bekommst einen besseren räumlichen Eindruck)
Die Gerade \(h\) schneidet die Ebene \(E\) im Punkt \(S=(4|\,0|\,2)\)
... und die durch orthogonale Projektion von h auf E entsteht.
"orthogonale Projektion" bedeutet, dass jeder Punkt (jetzt von \(h\)) senkrecht (orthogonal) auf die Ebene projiziert wird. Man lässt jeden Punkt praktisch auf die Ebene runter plumsen. Wo 'unten' ist, wird durch die Ebene definiert. Es ist die kürzeste Strecke von dem Punkt zur Ebene und die 'Plumsrichtung' ist immer senkrecht zur Ebene.Ich habe Dir das durch die lila Pfeile veranschaulicht (s.o.).
Da die Projektion selbst wieder eine Gerade ist, reicht es aus, zwei Punkte der ursprünglichen Gerade zu wählen und ihre Projektion zu berechnen. Das kann man z.B. erreichen indem man den Normalenvektor der Ebene - der ja senkrecht drauf steht - als Richtungsvektor einer Hilfsgerade wählt. Und anschließend einen Punkt der Geraden als Stützpunkt der Hilfsgeraden. Der Schnittpunkt der Hilfsgeraden mit der Ebene ist dann die Projektion des Punktes.