kubische Gleichung mit Wurzel lösen

Question

Aufgabe:

Ich scheitere beim Versuch einer Polynom-Division

\( x^{3}-\sqrt{3} x^{2}-3 x+1 / 3 \sqrt{3}=\tan 10^{\circ} \)

Problem/Ansatz:

Ich versuche es mit Polynomdivision, scheitere aber. Versucht mit /(x+sqrt(3), klappt aber nicht. Bitte um Hilfe.danke...

Comments

Sicher, dass die Gleichung richtig abgeschrieben ist?

Würde die Gleichung

\( x^{3}-\sqrt{3} x^{2}-3 x+1 / 3 \sqrt{3}=0 \)

lauten, so wäre die Lösung \(x=\tan 10^{\circ}\).

---

Die Lösung ist wohl nicht ganz korrekt. \(x_2=\tan 70^\circ\), sowie \(x_3=\tan 130^\circ\) lösen die Gleichung ebenfalls.

---

Deinem Einwand stimme ich zu.

Answer 1

Hallo,

$$ x^{3}-\sqrt{3} x^{2}-3 x+\frac{1}{3} \sqrt{3}=\tan 10^{\circ} $$

die Gleichung ist IMHO so nicht faktorisierbar. D.h. Du wirst keinen Term \((x-a)\) finden mit einer algebraischen Zahl \(a\) die ein Faktor dieses Ausdrucks ist.

Bleiben die Cardanischen oder besser gleich Newton. Näherungslösungen sind:$$x_{1,2,3}\approx\left\{-1,1579144193;\,0,125269634921;\,2,76469559195\right\}$$

Comments

Wolframalpha:

https://www.wolframalpha.com/input?i=x%5E3+-+%E2%88%9A3%C2%B7x%5E2+-+3%C2%B7x+%2B+1%2F3%C2%B7%E2%88%9A3+%3D+TAN%2810%C2%B0%29

Answer 2

Das erinnert mich an das Additionstheorem für tan(3x).

Versuche mal den Term für tan(3*10°) danach aufzustellen.

Comments

Meinst du

$$\tan(3x) = \frac{3 \tan(x) - \tan^3(x)}{1-3 \tan^2(x)}$$

---

Das erinnert mich an das Additionstheorem für tan(3x).

Was soll das hier bringen?

---

Das erinnert mich an das Additionstheorem für tan(3x).

Mal probieren ...$$\tan(x+x) = \frac{2\tan(x)}{1-\tan^2(x)} \\ \begin{aligned} \tan(3x) &= \frac{\tan(2x) + \tan(x)}{1-\tan(2x)\tan(x)} \\ &= \frac{\frac{2\tan(x)}{1-\tan^2(x)} + \tan(x)}{1-\frac{2\tan(x)}{1-\tan^2(x)}\tan(x)} \\ &= \frac{2\tan(x) + \tan(x) -\tan^3(x)}{1-\tan^2(x)-2\tan^2(x)} \\ &= \frac{3\tan(x) -\tan^3(x)}{1-3\tan^2(x)} \\ \end{aligned}$$.. und weiter:$$\tan(30°) = \frac{1}{3}\sqrt{3}$$bzw.:$$\begin{aligned}\frac{1}{3}\sqrt{3}&= \frac{3\tan(10°) -\tan^3(10°)}{1-3\tan^2(10°)}\\\frac{1}{3}\sqrt{3}\left(1-3\tan^2(10°)\right) &= 3\tan(10°) - \tan^3(10°)\\  \tan^3(10°) - \sqrt{3}\tan^2(10°)-3\tan(10°) + \frac{1}{3}\sqrt{3} &=0\end{aligned}$$Ok - aber auf der rechten Seite der ursprünglichen Gleichung steht noch ein Wert \(\ne 0\). Was nun?

---

Ich habe wahrscheinlich bei der Aufgabenstellung einen Fehler begangen.

Die Aufgabe heißt im Original:

Hence show that tan10° is a root of the equitation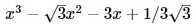

Text erkannt:

\( x^{3}-\sqrt{3} x^{2}-3 x+1 / 3 \sqrt{3} \)

Sorry dafür. Ich ging davon aus, dass tan10° die Lösung der Gleichung ist.

"abakus" hat mir sehr geholfen

---

Offensichtlich war das nicht der einzige Fehler, denn was du hingeschrieben hast, ist nur ein Term und keine Gleichung.