Aufgabe:
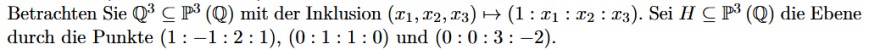
Text erkannt:
Betrachten Sie \( \mathbb{Q}^{3} \subseteq \mathbb{P}^{3}(\mathbb{Q}) \) mit der Inklusion \( \left(x_{1}, x_{2}, x_{3}\right) \mapsto\left(1: x_{1}: x_{2}: x_{3}\right) \). Sei \( H \subseteq \mathbb{P}^{3}(\mathbb{Q}) \) die Ebene durch die Punkte \( (1:-1: 2: 1),(0: 1: 1: 0) \) und \( (0: 0: 3:-2) \).

Text erkannt:
Sei \( H_{\infty}=\mathbb{P}^{3}(\mathbb{Q}) \backslash \mathbb{Q}^{3} \) die Ebene im Unendlichen und \( L \subseteq \mathbb{P}(\mathbb{C})^{3} \) der projektive Abschluss der Gerade \( (0,1,-1)+\mathbb{Q}(1,0, a) \subseteq \mathbb{Q}^{3} \). Für welche Werte von \( a \) ist \( L \cap H \in H_{\infty} \) ?
Problem/Ansatz:
$$H=-9x_0-2x_1+2x_2+3x_3$$
Ich habe mir aus der Geraden 2 Punkte genommen $$(0,1,-1)$$ und $$(1,1,-1+a)$$ habe dann den projektiven Abschluss gebildet: $$(1:0:1:-1)$$ und $$(1:1:1:-1+a)$$ dann sollen diese ja die Gleichung $$Ax_0+Bx_1+Cx_2+Dx_3 = 0$$ erfüllt sein. Dann habe ich ein LGS aus den beiden $$(1:0:1:-1)$$ und $$(1:1:1:-1+a)$$ gemacht und dieses versucht zu lösen. DIe einfachste Lösung war $$x_0-x_2 = 0$$ dann habe ich mit dieser und der für H ein LGS gebildet und das gelöst, wobei der Schnitt dann (1:-2:1:1) ist.
Ich bin mir hier sehr unsicher ob das so richtig ist und wäre froh drüber wenn jemand mich korrigieren kann :)