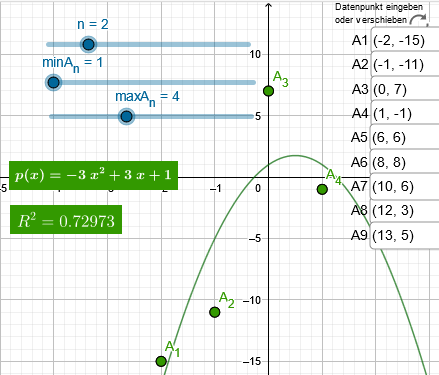
für \(f(x) \, := \, a_2 \; x^{2} + a_1 \; x + a_0\)
Du hast in der 2. Zeile einen Fehler und wo ist γ(a_0)
\(\small \left(\begin{array}{rrr}4&-2&1\\1&-1&1\\0&0&1\\1&1&1\\\end{array}\right) \left(\begin{array}{r}a_2\\a_1\\a_0\\\end{array}\right)= \left(\begin{array}{r}-15\\-11\\7\\-1\\\end{array}\right) \)
\( A \vec{a_i}=b \to Normalengleichung\, A^T A\, \vec{a_i} = A^T b \to \vec{a_i}\)
und keine Normalengleichung erstellt
\(\small \left\{ \left(\begin{array}{rrr}18&-8&6\\-8&6&-2\\6&-2&4\\\end{array}\right) \left(\begin{array}{r}a_2\\a_1\\a_0\\\end{array}\right)= \left(\begin{array}{r}-72\\40\\-20\\\end{array}\right) \right\} \)
siehe
https://www.geogebra.org/m/BpqJ28eP#material/YjjE9nwR