Aufgabe:
Untersuchen Sie die folgenden Funktionen auf Beschränktheit (nach oben und unten) und auf Monotonie.
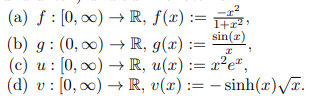
Text erkannt:
(a) \( f:[0, \infty) \rightarrow \mathbb{R}, f(x):=\frac{-x^{2}}{1+x^{2}} \),
(b) \( g:(0, \infty) \rightarrow \mathbb{R}, g(x):=\frac{\sin (x)}{x} \),
(c) \( u:[0, \infty) \rightarrow \mathbb{R}, u(x):=x^{2} e^{x} \),
(d) \( v:[0, \infty) \rightarrow \mathbb{R}, v(x):=-\sinh (x) \sqrt{x} \).
Problem/Ansatz:
Wie soll ich hier grundsätzlich vorgehen? Rein logisch gesehen würde ich vermuten das a) durch 0 und 1 beschränkt ist, aber wie soll ich da grundsätzlich vorgehen? Auch für die Monotonie brauche ich einen Tipp. Kann ich da irgendwas mit Ableitungen machen?