Aufgabe: Bestimmen Sie die folgenden Integrale.

Text erkannt:
(b) \( \int \frac{1}{\sqrt{1+x^{2}}} \mathrm{~d} x \)
Tipp: Verwenden Sie in (b) die Substitution x = sinh t
Problem/Ansatz:
Ich habe die Lösung, verstehe sie aber nicht vollends.
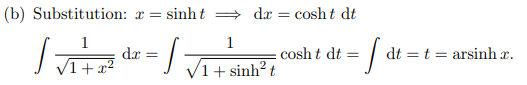
Text erkannt:
(b) Substitution: \( x=\sinh t \Longrightarrow \mathrm{d} x=\cosh t \mathrm{~d} t \)
\( \int \frac{1}{\sqrt{1+x^{2}}} \mathrm{~d} x=\int \frac{1}{\sqrt{1+\sinh ^{2} t}} \cosh t \mathrm{~d} t=\int \mathrm{d} t=t=\operatorname{arsinh} x \)
Ich verstehe den letzten Schritt quasi nicht. Wie kommen wir da auf dt=t=arsinh x? Der Anfang ist ja nur einsetzen.