Auflösung komplexer Doppelbruch

Question

Aufgabe:

Auflösung komplexer Doppelbruch

Problem/Ansatz:

ich stehe mathemathisch vor folgender Herausforderung. Der Doppelbruch soll so gut es geht vereinfacht werden.

Anbei die Angabe + Lösungsansatz

Bitte um Kontrolle, ob meine Lösung so korrekt sein kann bzw. ob man zur idealen Endform mathemathisch überhaupt kommen kann (das entspräche der gesuchten Standardform)

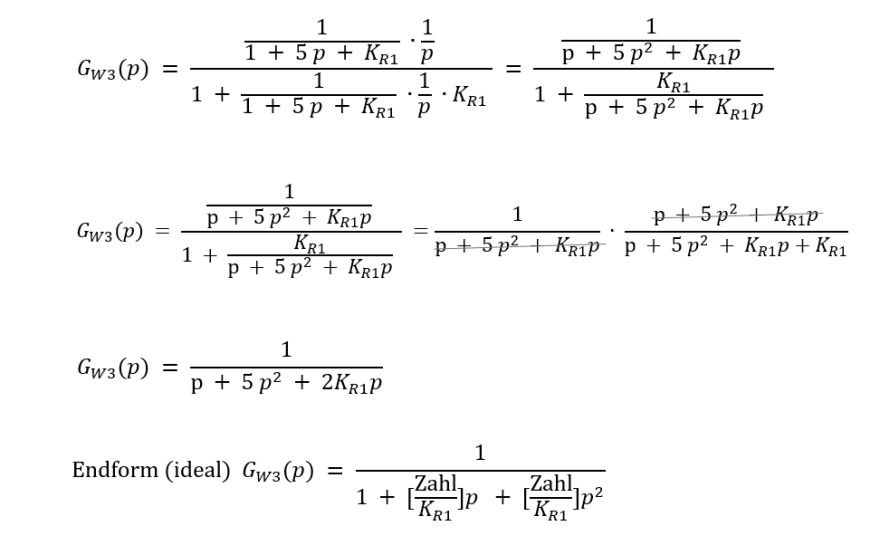
Text erkannt:

\( G_{W 3}(p)=\frac{\frac{1}{1+5 p+K_{R 1}} \cdot \frac{1}{p}}{1+\frac{1}{1+5 p+K_{R 1}} \cdot \frac{1}{p} \cdot K_{R 1}}=\frac{\frac{1}{\mathrm{p}+5 p^{2}+K_{R 1} p}}{1+\frac{K_{R 1}}{\mathrm{p}+5 p^{2}+K_{R 1} p}} \)
\( G_{W 3}(p)=\frac{\frac{1}{\mathrm{p}+5 p^{2}+K_{R 1} p}}{1+\frac{K_{R 1}}{\mathrm{p}+5 p^{2}+K_{R 1} p}}=\frac{1}{\mathrm{p}+5 p^{2}+K_{R 1} p} \cdot \frac{\mathrm{p}+5 p^{2}+K_{R 1} p}{\mathrm{p}+5 p^{2}+K_{R 1} p+K_{R 1}} \)
\( G_{W 3}(p)=\frac{1}{\mathrm{p}+5 p^{2}+2 K_{R 1} p} \)
Endform (ideal) \( G_{W 3}(p)=\frac{1}{1+\left[\frac{\mathrm{Zahl}}{K_{R 1}}\right] p+\left[\frac{\mathrm{Zahl}}{K_{R 1}}\right] p^{2}} \)

Answer 1

Aloha :)

$$G_{W3}(p)=\frac{\frac{1}{\pink{1+5p+K_{R1}}}\cdot\frac{1}{\pink p}}{1+\frac{1}{\pink{1+5p+K_{R1}}}\cdot\frac{1}{\pink p}\cdot K_{R1}}=\frac{\frac{1}{\pink{1+5p+K_{R1}}}\cdot\frac{1}{\pink p}\cdot\green{(1+5p+K_{R1})p}}{\left(1+\frac{1}{\pink{1+5p+K_{R1}}}\cdot\frac{1}{\pink p}\cdot K_{R1}\right)\cdot\green{(1+5p+K_{R1})p}}$$$$\phantom{G_{W3}(p)}=\frac{1}{1\cdot\green{(1+5p+K_{R1})p}+K_{R1}}=\frac{1}{p+5p^2+(1+p)K_{R1}}$$

Answer 2

Hallo,

Nenner:

\( \mathrm{p}+5 p^{2}+K_{R 1} p+K_{R 1} \)  ≠  \( \mathrm{p}+5 p^{2}+2 K_{R 1} p \)

Ich komme nicht auf die Endform.

Ansonsten habe ich den Weg auch so, wie Du.