Aufgabe:
Seien f,b: R->R mit einer stetigen Funktion b, für die b(0)=0 gilt. Weier gelte |f(x)|<=µ|x|b(x) für eine reelle Zahl µ>= 0. Zeigen Sie, dass f in 0 differenzierbar ist mit f´(0)=0
Hinweis: Argumentieren Sie mit dem DIfferenzenquotienten von f.
Problem/Ansatz:
Ich hatte mal eine ähnliche Aufgabe wo der Lösungsweg so aussah:
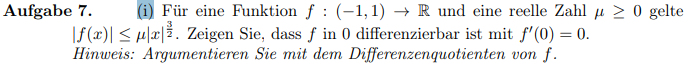
Text erkannt:
Aufgabe 7 .
(i) Für eine Funktion \( f:(-1,1) \rightarrow \mathbb{R} \) und eine reelle Zahl \( \mu \geq 0 \) gelte \( |f(x)| \leq \mu|x|^{\frac{3}{2}} \). Zeigen Sie, dass \( f \) in 0 differenzierbar ist mit \( f^{\prime}(0)=0 \).
Hinweis: Argumentieren Sie mit dem Differenzenquotienten von \( f \).
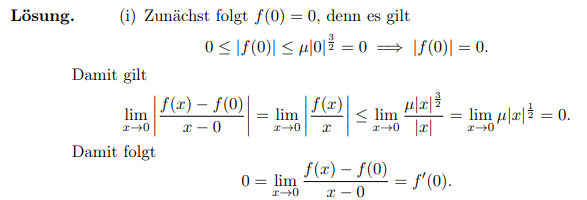
Text erkannt:
Lösung.
(i) Zunächst folgt \( f(0)=0 \), denn es gilt
\( 0 \leq|f(0)| \leq \mu|0|^{\frac{3}{2}}=0 \Longrightarrow|f(0)|=0 . \)
Damit gilt
\( \lim \limits_{x \rightarrow 0}\left|\frac{f(x)-f(0)}{x-0}\right|=\lim \limits_{x \rightarrow 0}\left|\frac{f(x)}{x}\right| \leq \lim \limits_{x \rightarrow 0} \frac{\mu|x|^{\frac{3}{2}}}{|x|}=\lim \limits_{x \rightarrow 0} \mu|x|^{\frac{1}{2}}=0 . \)
Damit folgt
\( 0=\lim \limits_{x \rightarrow 0} \frac{f(x)-f(0)}{x-0}=f^{\prime}(0) . \)
Deswegen meine Frage: Wie muss ich diese Lösung modifizieren um meine Aufgabe korrekt zu lösen? Ich dachte ich fange erstmal genauso an, also zeige das |f(0)|=0 (oder ist das hier nicht nötig)
Dann mache ich genauso weiter nur wo µ|x| 3/2 steht schreibe ich µ|x|b(x) hin (oder ohne das b(x)?). Daraus folgt dann für limes x->0 µ|x| =0. Der Rest ist wieder gleich. Stimmt das so oder was muss ich noch ändern/anders ändern?