Hallo Community,
kann mir jemand bitte erklären wie man auf den letzten Schritt kommt? Vor allem, woher die Wurzel herkommt...
Bitte mit Rechenschritten.
Vielen lieben Dank schon einmal!
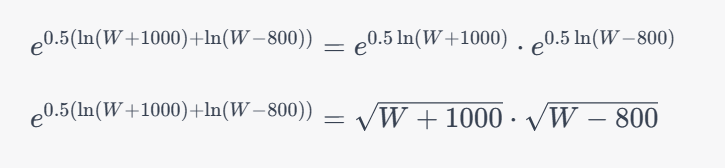
Text erkannt:
\( \begin{array}{l}e^{0.5(\ln (W+1000)+\ln (W-800))}=e^{0.5 \ln (W+1000)} \cdot e^{0.5 \ln (W-800)} \\ e^{0.5(\ln (W+1000)+\ln (W-800))}=\sqrt{W+1000} \cdot \sqrt{W-800}\end{array} \)