a) Der Graph einer ganzrationalen Funktion dritten Grades hat im Koordinatenursprung ein lokales Minimum. Er verläuft durch den Punkt \( \mathrm{P}(3|90) \) und hat bei \( x=7 \) ein lokales Maximum.
Bestimmen Sie den Funktionsterm \( f(x) \).
In einer ländlichen Region tritt eine Krankheit auf, deren Ausbreitung durch die Funktion f(t) = -4/3 t^{3} + 14 t^{2} beschrieben werden kann. (t: Tage nach erstmaligem Auftreten der Krankheit; f(t): Anzahl der Neu-Infektionen am Tag t)
Alle Erkrankten gehen direkt zum Arzt und lassen sich behandeln, nach vier Tagen sind sie wieder gesund.
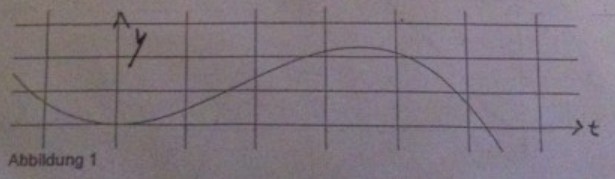
In Abbildung 1 ist der Graph von \( f(t) \) - ohne Skalierung der beiden Achsen - skizziert.
b) Berechnen Sie \( f(3) \) und geben Sie die Bedeutung des Ergebnisses im Sachzusammenhang an.
c) Ermitteln Sle einen sinnvollen Definitionsbereich für \( f(t) \) und geben Sie den Zeitpunkt an, an dem niemand mehr krank ist.
d) In der Region befinden sich fünf Arztpraxen, die täglich (auch am Wochenende) jeweils bis zu 50 Patlenten behandeln können. Untersuchen Sie, ob die ärztiche Versorgung gewährleistet ist.
e) Bestimmen Sie den Zeitpunkt, an dem die Neuinfektionsrate am stärksten zunimmt.
f) Wie auf der Abbildung 1 zu sehen ist, steigt die Anzahl der Infektionen zu Beginn stark an. Bestimmen Sie die durchschnittiche Zuwachsrate (pro Tag) der Neuinfektionen während der ersten Woche.
g) In einer dichter besiedelten (städtischen) Umgebung nimmt die Ausbreitung der Krankheit einen analogen zeitlichen Verlauf. Da dort aber drei Mal so viele Menschen leben, werden auch drei Mal so viele Menschen krank. Ergânzen Sie Abbildung 1 entsprechend und geben Sle einen dazu passenden Funktionsterm \( \mathrm{g}(t) \) an.