Berechnen Sie den Schnittpunkt

Question

Aufgabe:

Die Geraden g und h schneiden sich. Berechnen Sie den Schnittpunkt.

Problem/Ansatz:

Wir sollten uns an der Aufgabe nur probieren. Da ich sie aber gerne verstehen würde, würde ich mich sehr über Hilfe freuen, weil ich trotz Versuchen keine Idee habe:

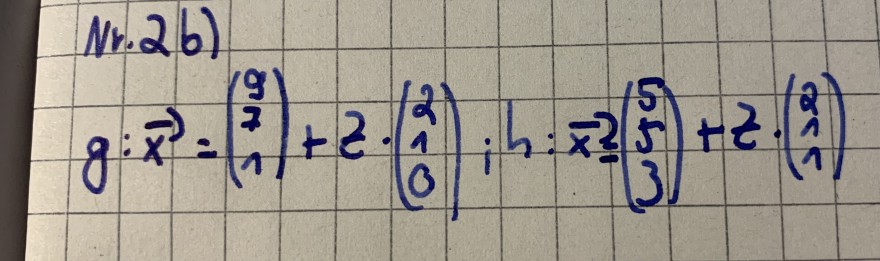
Text erkannt:

Nr.26)
\( g: \vec{x}=\left(\begin{array}{l} 9 \\ 7 \\ 1 \end{array}\right)+z \cdot\left(\begin{array}{l} 2 \\ 1 \\ 0 \end{array}\right) ; h: \vec{x}\left(\begin{array}{l} 5 \\ 5 \\ 3 \end{array}\right)+z \cdot\left(\begin{array}{l} 2 \\ 1 \\ 1 \end{array}\right) \)

Ich habe es nur abfotografiert, weil ich nicht weiß, wie ich das hier sonst sichtbar machen kann.

Comments

Finde \(a,b\in\R\) mit \(\begin{pmatrix}9\\7\\1\end{pmatrix}+a\cdot\begin{pmatrix}2\\1\\0\end{pmatrix}=\begin{pmatrix}5\\5\\3\end{pmatrix}+b\cdot\begin{pmatrix}2\\1\\1\end{pmatrix}\). Lösung: \(a=-4\) und \(b=-2\).

Answer 1

Hallo,

Für jeden Punkt \(S\) auf der Geraden \(g\) gibt es einen Wert \(z_g\), der eingesetzt in die Geradengleichung für \(g\) genau diesen Punkt ergibt:$$g: \quad \vec{x}=S(z_g)=\begin{pmatrix} 9 \\ 7 \\ 1 \end{pmatrix}+z_g \cdot\begin{pmatrix} 2 \\ 1 \\ 0 \end{pmatrix}$$das gleiche gilt für die Gerade \(h\). Wenn es also einen Schnittpunkt \(S\) gibt - also einen Punkt, der auf beiden Geraden liegt, so gibt es einen Punkt$$S(z_g)= S(z_h)$$Folglich suchen wir eine Lösung für $$\begin{pmatrix} 9 \\ 7 \\ 1 \end{pmatrix}+z_g \cdot\begin{pmatrix} 2 \\ 1 \\ 0 \end{pmatrix} = \begin{pmatrix}5\\ 5\\ 3\end{pmatrix} + z_h \cdot \begin{pmatrix}2\\ 1\\ 1\end{pmatrix}$$etwas umformatieren ergibt:$$\begin{pmatrix}2\\ 1\\ 0\end{pmatrix} \cdot z_g + \begin{pmatrix}-2\\ -1\\ -1\end{pmatrix} \cdot z_h = \begin{pmatrix}5\\ 5\\ 3\end{pmatrix} - \begin{pmatrix}9\\ 7\\ 1\end{pmatrix} = \begin{pmatrix}-4\\ -2\\ 2\end{pmatrix}$$bzw. als Matrix-Gleichung geschrieben:$$\begin{pmatrix}2& -2\\ 1& -1\\ 0& -1\end{pmatrix}\cdot \begin{pmatrix}z_g\\ z_h\end{pmatrix} = \begin{pmatrix}-4\\ -2\\ 2\end{pmatrix}$$Dieses Gleichungssystem ist überbestimmt, d.h. es ist i.A. eine von drei Gleichungen zu viel für zwei Unbekannte. Man löst es daher nur für zwei Gleichungen, hier bieten sich die zweite und dritte Gleichung an, die man einfach von einander abzieht:$$\begin{aligned}z_g - z_h &= -2 \\ -z_h &= 2\end{aligned}\\ \implies z_g = -4$$Daraus folgt dann auch gleich \(z_h = -2\) und Einsetzen dieses Lösungspaars in die dritte verbleibende Gleichung bestätigt, dass das System lösbar ist.

Einsetzen von \(z_h=-2\) in die zweite Geradengleichung liefert:$$S(z_h=-2) = \begin{pmatrix}5\\ 5\\ 3\end{pmatrix} + (-2) \begin{pmatrix}2\\ 1\\ 1\end{pmatrix} = \begin{pmatrix}1\\ 3\\ 1\end{pmatrix}$$Und zur Bestätigung das ganze in Geoknecht3D:

(klick drauf)

Gruß Werner

Comments

Vielen Dank für die Hilfe und Erklärungen! VG