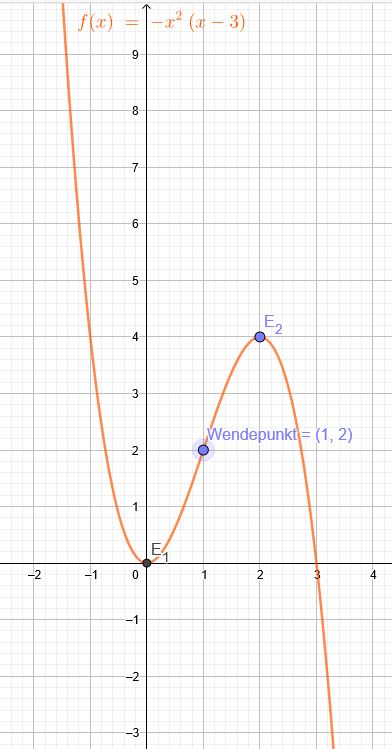
Der Graph einer ganz rationalen Funktion dritten Grades hat im Ursprung und im Punkt \(P(2|4)\) jeweils ein Extremum. wie lautet die Funktionsgleichung?
Ganz rationale Funktionen dritten Grades sind symmetrisch zum Wendepunkt, somit liegt der Wendepunkt in \(W(1|2)\)
\(f(x)=a*x^2*(x-N)\)
\(P(2|4)\)
\(f(2)=a*2^2*(2-N)=4a*(2-N)=4\) \(a=\frac{1}{2-N}\)
\(f(x)=\frac{1}{2-N}*x^2*(x-N)\)
\(W(1|2)\)
\(f(1)=\frac{1}{2-N}*1^2*(1-N)=2\) \(N=3\) \(a=\frac{1}{2-3}=-1\)
\(f(x)=-x^2*(x-3)\)