Hallo,
... die vorgeschlagenen Artikel gehen von der Existenz einer Rotationsmatrix aus. Was ich in meinem Fall aber habe, ist ein Beschleunigungssensor in Ruhe, aber in beliebiger Schieflage.
und damit kannst Du auf Teile der Rotationsmatrix schließen.
Die Spalten der Rotationsmatrix sind die Raumrichtungen der lokalen Koordinatenachsen des rotierten Objekts. Die drei Beschleunigungswerte geben die drei Koordinaten des (negativen) Z-Vektors des Raums an, bezogen auf die lokalen Koordinaten des Objekts. Also die inverse Information.
Wenn man also die Rotationsmatrix invertiert, entspricht die dritte Spalte (die Z-Achse) der Inversen der Richtung der Z-Achse im Raum aus Sicht des Objekts und damit genau der Richtung, die Dir die Beschleunigungssensoren liefern. Glücklicherweise sind Rotationsmatrizen orthogonale Matrizen, deren Inverse gleich ihrer Transponierten ist. Somit ist die Z-Richtung des Raums bezogen auf das Objekt die dritte Zeile der Ausgangsmatrix. Sind die Werte \(b_x\), \(b_y\) und \(b_z\) die drei gemessenen Beschleunigungen, so folgt daraus und aus dieser Matrix:$$\begin{pmatrix} b_x\\ b_y\\ b_z \end{pmatrix} = -g \begin{pmatrix} -\sin(\beta)\\ \cos(\beta)\sin(\gamma)\\\cos(\beta)\cos(\gamma) \end{pmatrix}$$Daraus lässt sich dann der Nickwinkel \(\beta\) und Rollwinkel \(\gamma\) in der dort beschriebenen Weise berechnen. Bei der Berechnung sollte man ausnutzen, dass die Länge des Vektors rechts (ohne \(-g\cdot\)) gleich 1 ist.
Ich suche nach einer guten Möglichkeit graphisch darzustellen, wie roll und pitch eines Beschleunigungssensors nur durch Anwendung von etwas Trigonometrie und Pythagoras ermittelt werden können.
Das ist nicht einfach. Ich habe da mal was im Geoknecht3D skizziert:
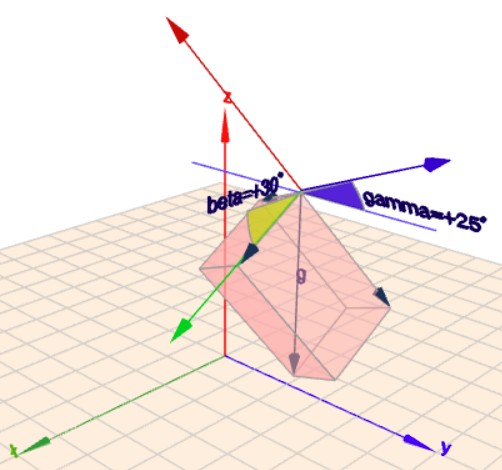
Wenn Du auf das Bild klickst, dann öffnet sich die Webseite vom Geoknecht3D und Du kannst die Szene mit der Maus rotieren. So kommt das 3-dimensionale deutlich besser zu Geltung.
Das Gebilde, welches dort im Raum über der Ebene schwebt, soll ein Objekt darstellen, mit dem Nickwinkel \(\beta\) (grün) und den Rollwinkel \(\gamma\) (blau). Der schwarze Vektor \(g\), der senkrecht nach unten zeigt, soll die Erdbeschleunigung darstellen. Ein (oder mehrere) Beschleunigunssensor im Objekt messen nun die drei Beschleunigungen im Koordinatensystem des Objekts. Das habe ich versucht durch den den achsenparallelen Quader darzustellen. Die drei Kanten des Quaders, die die Ecke im Koordinatenursprung des Objekts gemeinsam haben, bilden die drei gemessenen Beschleunigungen ab.
Wenn man nun eine ZX-Ebene im Raum(!) betrachtet, die durch den Ursprung des Objekts geht, so ergibt sich folgendes Bild:
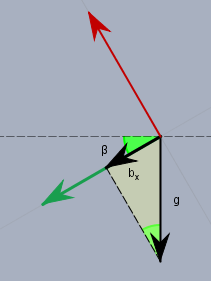
Der Winkel \(\beta\) taucht in dem Dreieck, was durch \(g\) und \(b_x\) gebildet wird, wieder auf. Und es gilt offensichtlich$$\sin(\beta) = \frac{b_x}{|g|} \quad |g|=\sqrt{b_x^2+b_y^2+b_z^2}$$Womit \(\beta\) zu berechnen wäre.
Mit \(\gamma\) ist es nicht ganz so einfach. Für den Rollwinkel \(\gamma\) betrachte ich die YZ-Ebene des Körpers, was der rückwärtigen Fläche des Quaders entspricht.
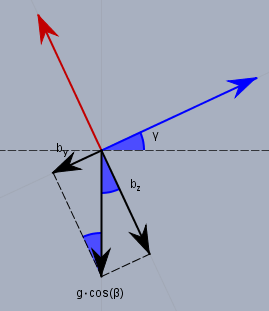
Der Vektor, der nach unten zeigt, ist nun nicht \(g\) sondern die Projektion von \(g\) auf eben diese rückwärtige Fläche. Und da die Fläche um \(\beta\) gekippt ist, hat der Vektor den Betrag \(|g|\cos(\beta)\). Der (oder die) Beschleunigungssensor misst nun anteilig die Werte in Richtung der (negativen) Achsen des objektfesten Koordinatensystems. Und hier gilt$$b_y = -|g|\cdot \cos(\beta) \cdot \sin(\gamma) \\ b_z = -|g|\cdot \cos(\beta) \cdot \cos(\gamma)$$woraus sich wiederum mit der Kenntnis von \(|g|\) und \(\beta\) der Rollwinkel \(\gamma\) eindeutig berechnen lässt.
Bitte melde Dich, falls Du dazu noch Fragen oder sonstigen Bemerkungen hast. Ich freue mich über jedes Feedback ;-)
Gruß Werner