Fläche unter dem Graphen bestimmen. Wie?

Question

Aufgabe:

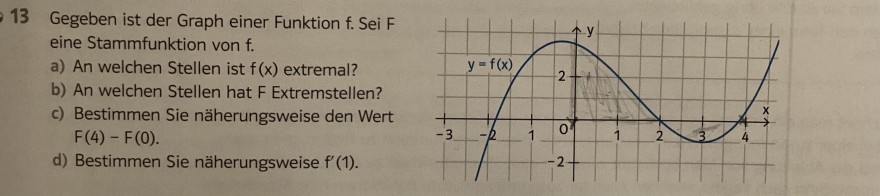
Text erkannt:

13 Gegeben ist der Graph einer Funktion f. Sei F eine Stammfunktion von \( f \).
a) An welchen Stellen ist \( f(x) \) extremal?
b) An welchen Stellen hat F Extremstellen?
c) Bestimmen Sie näherungsweise den Wert \( F(4)-F(0) \)
d) Bestimmen Sie näherungsweise \( f^{\prime}(1) \).

…

Problem:

Welche Fläche wird bei der c) gemeint von 0 bis 4 und wie viel beträgt diese? Wie geht man hier vor?

Answer 1

Welche Fläche wird bei der c) gemeint von 0 bis 4 und wie viel beträgt diese? Wie geht man hier vor?

Die Bilanzfläche lässt sich näherungsweise durch Kästchenzählen bestimmen. Die Flächen sind ja bereits markiert. Teilflächen unterhalb der x-Achse gehen negativ in die Bilanz ein.

Comments

Von 0 bis 2 sind es ungefähr fast 8 Kästchen und von 2 bis 4 sind es fast 2,5. werden diese Kästchen dann addiert? Und in den Lösungen steht bei mir 2,35 gerundet. Wieso das?

---

Nein, die Kästchen unterhalb der x-Achse gehen negativ in die Bilanz ein, sie müssen also subtrahiert werden.

---

Man kommt aber trotzdem nicht auf 2,35. ist die Lösung falsch? Oder verstehe ich das nicht ?

---

Das Zählergebnis muss noch mit der Größe eines Kästchens multipliziert werden.

---

Also habe jetzt links knapp 4 und rechts also die negative Fläche 1,5 ungefähr also kommt man auf 2,5 ungefähr. Ist es jetzt richtig?

---

\(\dots\approx (8-2.5)\cdot 0.5 = 2.75\)

---

Wieso noch mal 0.5 das verstehe ich nicht

---

Ein Kästchen in dem hier vorliegenden Koordinatensystem hat die Breite 0,5 Längeneinheiten und die Höhe 1 Längeneinheit. Das ergibt die Fläche (0,5 mal 1)=0,5 Flächeneinheiten.