Summe von i=0 bis n für i über k

Question

Aufgabe:

Beweise durch vollständige Induktion.

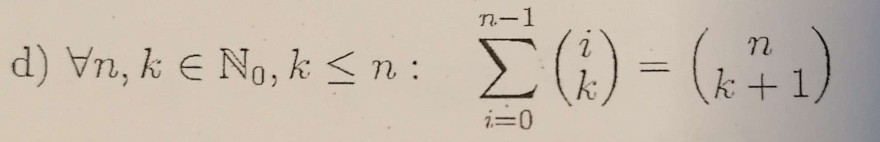
Problem/Ansatz:

Ich habe Induktionsanfang und Induktionsvoraussetzung geschaftt und die Induktionsbehauptung mit n->n+1 aufgestellt. Ich habe ein Problem mit der linken Seite der Gleichung:

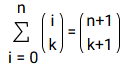
So kann ich ja nicht weiterrechnen, deshalb habe ich die linke Seite in Wolfram Alpha eingegeben.

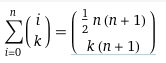
Ich weiß nicht, wie Wolfram Alpha das gelöst hat, es steht auch kein Rechenweg dabei. Ich könnte jetzt zwar meinen Induktionsbeweis damit fortsetzen, aber ich möchte verstehen, was ich rechne.

Comments

Praktisch treten Binomialkoeffizienten häufig in der Form auf, dass die obere Zahl größer gleich der unteren ist. Das ist hier nicht der Fall!? Wie habt Ihr dann die Binomialkoeffizienten definiert?

Answer 1

Du hast ja die Ind.Vor. schon aufgeschrieben. Vergleiche mit dieser linken Seite und Du stellst fest, dass diese linke Seite einen Summanden mehr als die linke Seite in der Ind.Vor.. Damit ist der erste Rechenschritt der Standardschritt in vielen Induktionen:

\(\sum\limits_{i=0}^n = \sum\limits_{i=0}^{n-1}+\) Summand für \(i=n\)

und nun wende die Ind. Vor. an und dann das Additionstheorem für Binomialkoeffizienten und man ist sofort fertig.

PS: Der von mathhilf angesprochene Punkt ist eine Überlegung wert. Wenn die Def. der BK aber so ist, dass das Additionstheorem gilt, dann kann man die Induktion wie eben gesagt leicht bewältigen.