Hallo,
die Aufgabe lautet wie folgt:
An der Uni wurde ein Experiment durchgeführt, um den Zusammenhang zwischen der täglichen Vorbereitungszeitung für Statistik und dem Abschneiden in einem Abschlusstest zu prüfen.
50 Studierende wurden per Zufall einer von fünf Untersuchungsbedingungen zugeteilt. (Gruppen a bis e):
Die Studierenden mussten über einen Zeitraum von 14 Wochen täglich (a) 0,25 Std., b) 0,5 Std., c) 1 Std., (d) 2 Std. bzw. (e) 3 Std. Statistikaufgaben bearbeiten.
Als abhängige Variable (y) wurde die Punktzahl in einem Abschlusstest erhoben.
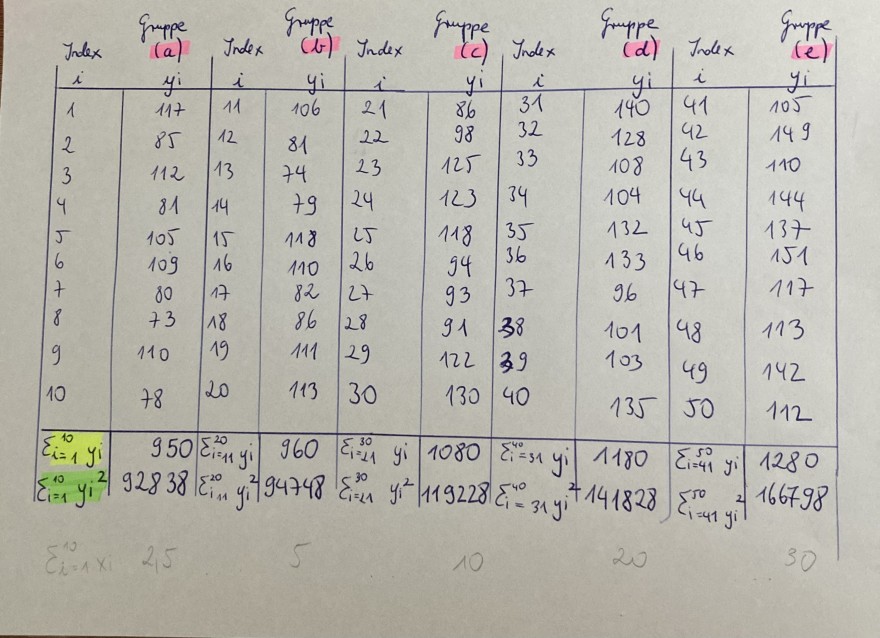
Die Ergebnisse und einzige Zwischenergebnisse für die fünf Gruppen sind in folgender Tabelle abgebildet:
(s. Anhang 1)
Nun soll die Regressionsgerade yi = a + bxi berechnet werden.
Mein Problem/ Ansatz:
Ich kann die Mittelwerte von x und y berechnen, komme allerdings danach nicht weiter. Wenn ich die erhaltenen Werte in die Formel für die Berechnung von b Dach einsetze, kommt definitiv etwas falsches heraus (s. Anhang 2)
b Dach soll sein: 12,32
Hoffe, jemand kann mir helfen!
Danke!
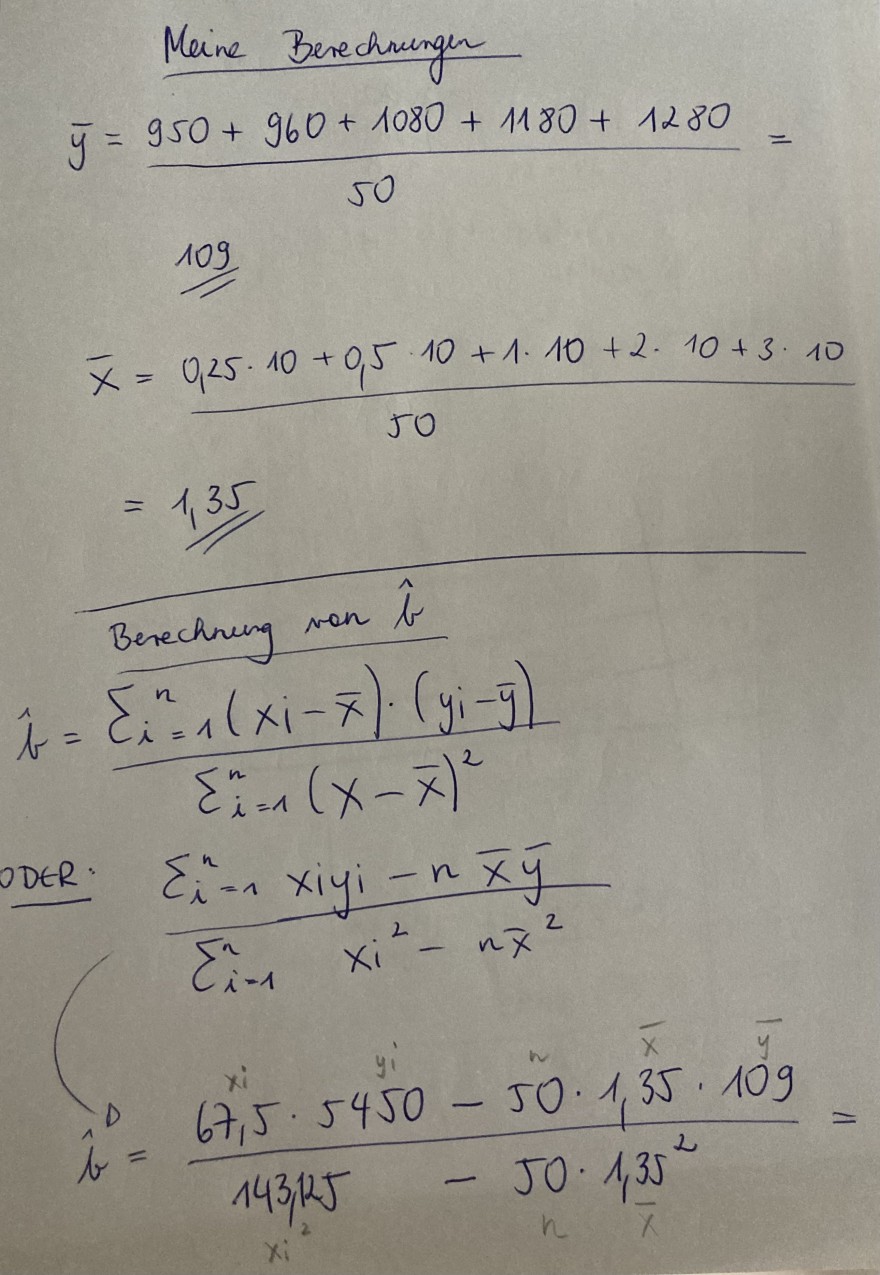
Text erkannt:
Meine Berechnungen
\( \bar{y}=\frac{950+960+1080+1180+1280}{50}= \)
109
\( \begin{aligned} \bar{x} & =\frac{0,25 \cdot 10+0,5 \cdot 10+1 \cdot 10+2 \cdot 10+3 \cdot 10}{50} \\ & =1,35 \end{aligned} \)
Berechneng von \( \hat{t} \)
\( \hat{b}=\frac{\sum \limits_{i=1}^{n}\left(x_{i}-\bar{x}\right) \cdot\left(y_{i}-\bar{y}\right)}{\sum \limits_{i=1}^{n}(x-\bar{x})^{2}} \)
ODER
\( \frac{\sum \limits_{i=1}^{n} x i y i-n \bar{x} \bar{y}}{\sum \limits_{i=1}^{n} x i^{2}-n \bar{x}^{2}} \)