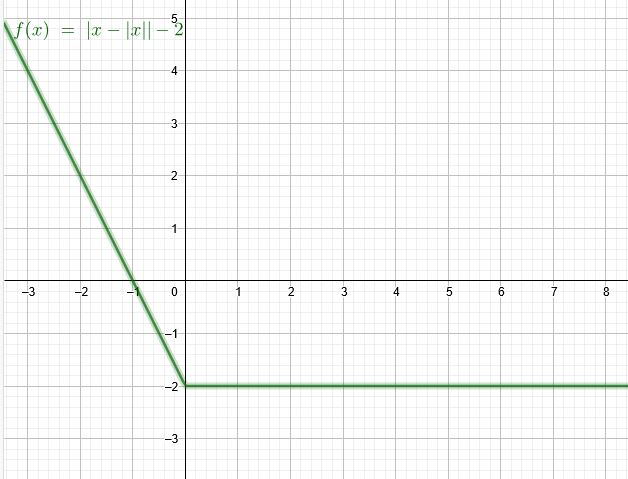
Ist zwar keine Antwort auf deine Frage gibt aber einen Lösungsweg:
\(|x-|x|| =2 | ^{2}\)
\((x-|x|)^2 =4 \)
\(x^2-2x|x|+x^2=4 \)
\(x^2-x|x|=2 \)
\(x|x|=x^2-2 | ^{2} \)
\(x^4=x^4-4x^2+4 \)
\(4x^2=4 \)
\(x_1=1 \)
\(x_2=-1 \)
Probe, da quadrieren keine Äquivalenzumformung ist:
1.) \(|1-|1|| =2 \) stimmt nicht
2.) \(|-1-|-1|| =2 \) stimmt