Text erkannt:
12:30 Samstag 11. Nov.
e-Funktionen
Prüfungsteil B: Aufgaben mit Hilfsmitteln
Aufgabenstellung
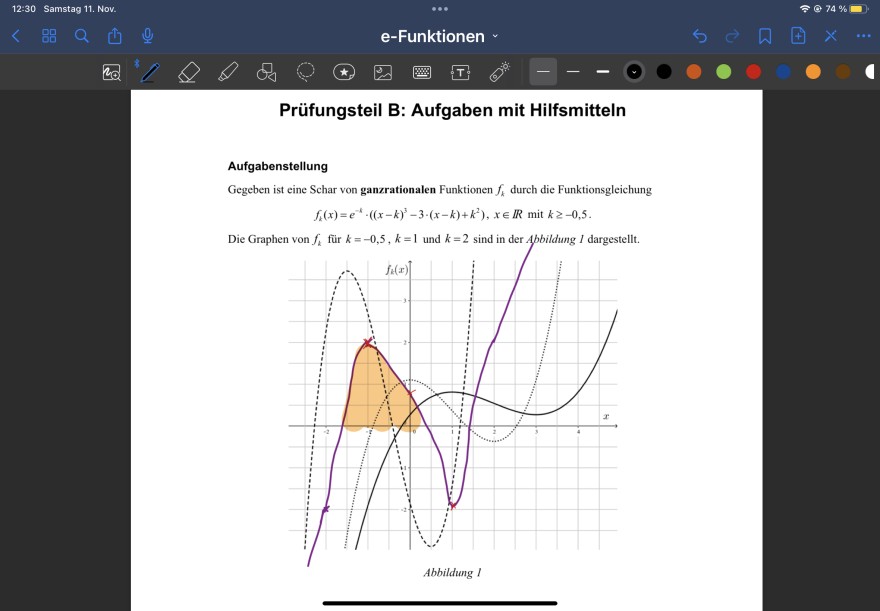
Gegeben ist eine Schar von ganzrationalen Funktionen \( f_{k} \) durch die Funktionsgleichung
\( f_{k}(x)=e^{-k} \cdot\left((x-k)^{3}-3 \cdot(x-k)+k^{2}\right), x \in \mathbb{R} \text { mit } k \geq-0,5 . \)
Die Graphen von \( f_{k} \) für \( k=-0,5, k=1 \) und \( k=2 \) sind in der Abbildung \( l \) dargestellt.
Abbildung I

Text erkannt:
b) Der lokale Hochpunkt des Graphen von \( f_{k} \) ist in Abhängigkeit von \( k \) gegeben durch \( H_{k}\left(k-1 \mid e^{-k} \cdot\left(2+k^{2}\right)\right) \).
Ermitteln Sie den Wert von \( k \) mit \( -0,5 \leq k \leq 10 \), für den der Abstand des Hochpunktes \( H_{k} \) zum Ursprung minimal ist.

Text erkannt:
Teilaufgabe b) Löscug
Für den gesuchten Abstand gilt: \( d(k)=\sqrt{(k-1)^{2}+\left(e^{-k} \cdot\left(2+k^{2}\right)\right)^{2}} \).
Gesucht ist der Wert \( k \) mit \( -0,5 \leq k \leq 10 \), für den der Abstand \( d(k) \) minimal ist.
Der Taschenrechner liefert \( k \approx 1,3 \).
[Auch eine grafische Analyse des Graphen von \( d \) mit dem Taschenrechner ist vorstellbar.]