Wie stelle ich da die Bedingungen auf?

Question

Aufgabe

Das Schaubild K einer ganzrationalen Funktion dritten Grades hat in H(0/4) und in T(4/-4)

Extrema.

Problem/Ansatz

Wie stelle ich da die Bedingungen auf?

Answer 1

Das Schaubild K einer ganzrationalen Funktion dritten Grades hat in H\((0|4)\) und in                T\((4|-4)\)Extrema.

\(f(x)=ax^3+bx^2+cx+d\)    Du benötigst somit 4 Bedingungen

1.)

H\((0|4)\) liegt auf dem Graphen

\(f(0)=a*0^3+b*0^2+c*0+d\)       → \(d=4\)

\(f(x)=ax^3+bx^2+cx+4\)

2.)

T\((4|-4)\) liegt ebenfalls auf dem Graphen

\(f(4)=a*4^3+b*4^2+c*4+4\)   →

 → \(a*4^3+b*4^2+c*4+4=-4\)   → \(a*4^3+b*4^2+c*4=-8\)  → \(a*4^2+b*4+c=-2\)

Die Extremstellen findest du mit \(f´(x)=0\)

3.)H\((0|...)\)

\(f´(x)=3ax^2+2bx+c\)

\(f´(0)=3a*0^2+2b*0+c\)    → \(c=0\)

4.)  T\((4|...)\)

\(f´(4)=3a*4^2+2b*4\)  →   \(3a*4^2+2b*4=0\)

Comments

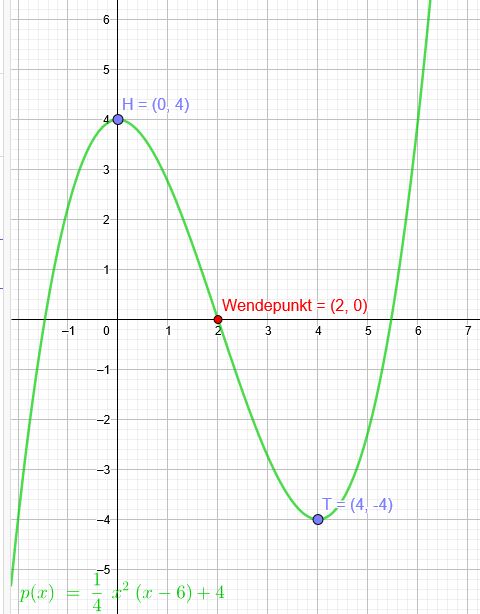
Das Schaubild K einer ganzrationalen Funktion dritten Grades hat in H\((0|4)\) und in T\((4|-4)\)Extrema.

Ein anderer Weg:

Ich verschiebe den Graphen um 4 Einheiten nach unten:

H\((0|4)\)→H´\((0|0)\)

\(f(x)=a*x^2*(x-N) \)

T\((4|-4)\)→T´\((4|-8)\)

\(f(4)=16a*(4-N)=-8 \)  →  \(a*(2N-8)=1 \)  →

→ \(a=\frac{1}{2N-8} \)

\(f(x)=\frac{1}{2N-8} *[x^3-N*x^2] \)

Extremstelle:

T´\((4|...)\)

\(f´(x)=\frac{1}{2N-8} *[3x^2-2N*x] \)

\(f´(4)=\frac{1}{2N-8} *[3*4^2-2N*4] \)

\(\frac{1}{2N-8} *[48-8N]=0 \)→\(N=6 \)

\(a=\frac{1}{2*6-8}=\frac{1}{4} \)

\(f(x)=\frac{1}{4} *x^2*(x-6) \)

um 4 Einheiten nach oben:

\(p(x)=\frac{1}{4} *x^2*(x-6) +4\)

Am Graphen siehst du auch recht deutlich die Punktsymmetrie.

Answer 2

f(0) = 4

f(4) = -4

f '(0) = 0

f '(4)= 0

Das sind die 4 Bedingungen für a,b,c.d

Answer 3

Benutze zur Hilfe und Selbstkontrolle https://www.arndt-bruenner.de/mathe/scripts/steckbrief.htm

Eigenschaften

f(0) = 4
f'(0) = 0
f(4) = -4
f'(4) = 0

Gleichungssystem

d = 4
c = 0
64a + 16b + 4c + d = -4
48a + 8b + c = 0

Errechnete Funktion

f(x) = 0,25·x^3 - 1,5·x^2 + 4