Fehlender Ansatz - DGL erster Ordnung

Question

Hallo Zusammen, bei der folgenden DGL scheine ich einen falschen Ansatz zu wählen. Ich würde y/x substituieren, was laut DGL Rechner allerdings falsch ist.

Wie lautet hier der richtige Ansatz?

Vielen Dank vorab!

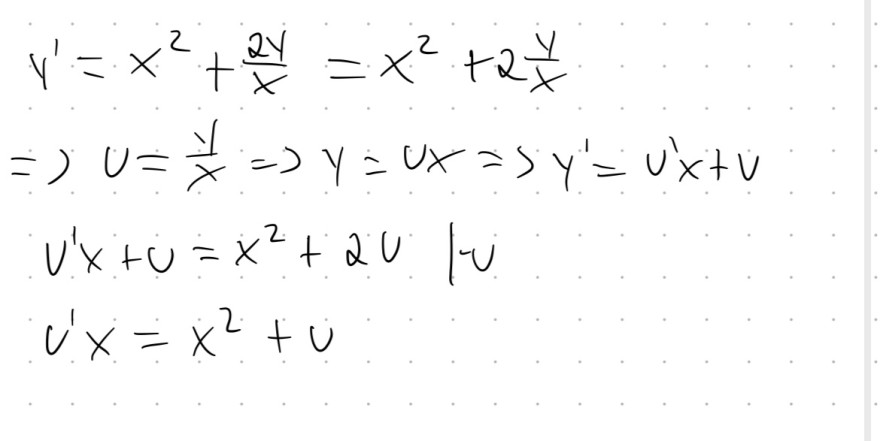
Text erkannt:

\( \begin{array}{l}y^{\prime}=x^{2}+\frac{2 y}{x}=x^{2}+2 \frac{y}{x} \\ \Rightarrow u=\frac{y}{x} \Rightarrow y=u x=5 y^{\prime}=u^{\prime} x+v \\ u^{\prime} x+u=x^{2}+2 u \quad \mid v \\ u^{\prime} x=x^{2}+u\end{array} \)

Comments

Der Ansatz $$y = \sum\limits_{k=0}^{n}a_{k}x^k$$ würde auch zum Ziel führen.

Answer 1

Hallo,

Das Problem kannst Du via Variation der Konstanten lösen.

y'=x^2 + (2y)/x | -(2y)x

y'  -(2y/x) = x^2

1.homogene DGL berechnen:
y' +A(x) y= 0->Trennung der Variablen

y'  -(2y/x) = 0

yh=C₁ x^2

2. Setze C1= C(x)
yp= C(x) x^2 
yp'= C'(x) *x^2 +C(x) *2x
3.Setze yp und yp' in die DGL ein

dabei muß C(x) herausfallen, wenn Du richtig gerechnet hast,

C(x)=
4. yp= C(x) * ......
5. y= yh+yp

Lösung: y=C₁ x^2 +x^3

Comments

Vielen Dank für die schnelle und hilfreiche Antwort. Wo liegt allerdings der Fehler, sodass bei mir ce^x^2 rauskommt?

Text erkannt:

\( \begin{array}{r}y^{\prime}-2 \frac{y}{x}=0\left|+2 \frac{y}{x}\right| d x \\ d y=\frac{2 y}{x} d x\left|\frac{1}{2 y}\right| \int \\ \int \frac{1}{2 y} d y=\int x d x=\frac{1}{2} \ln |y|=\frac{1}{2} x^{2}+c \mid 2 \\ \ln \left|y=x^{2}+c\right| e \\ y=c e^{x^{2}} \\ y=c x^{2}\end{array} \)

---

der Fehler liegt in der 3.Zeile.

Du mußt alles mit y auf eine Seite bringen, alles mit x auf die andere Seite

dy/y = (2/x) dx

Answer 2

Schaue Dir die Ableitung von \( \displaystyle {y\over x^2} \) an.