Wenn du diesen Zufallsprozess graphisch darstellen möchtest, eignet sich ein Prozessdiagramm:
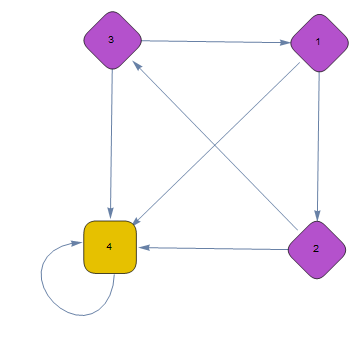
Hier stehen 1,2,3 für die Zustände: "Schütze 1,2,3 schießt" und 4 steht für "Hase erlegt". Kopier dir am besten den Graphen und ergänze die Wahrscheinlichkeiten an den Pfeilen.
In deinem Fall startet der Prozess bei 1.
Nun gibt es einen kleinen Trick, deine gesuchte Wahrscheinlichkeit zu berechnen.
Du berechnest zuerst die Wahrscheinlichkeiten \(p_i\), dass Schütze i den Hasen erlegt, wenn Schütze i auch mit dem Prozess startet:
Wenn Schütze 1 startet (wie im vorliegenden Fall):
\(p_1 = \frac34 + \frac14\cdot \frac 13\cdot \frac12\cdot p_1 =\frac 34 + \frac1{24}\cdot p_1 \Rightarrow p_1 = \frac{18}{23}\)
Wenn Schütze 2 startet:
\(p_2 =\frac 23 + \frac1{24}\cdot p_2 \Rightarrow p_2 = \frac{16}{23}\)
Wenn Schütze 3 startet:
\(p_3 =\frac 12 + \frac1{24}\cdot p_3 \Rightarrow p_3 = \frac{12}{23}\)
Jetzt musst du nur noch beachten, dass der Prozess für Schütze 2 nur mit der Wahrscheinlichkeit \(\frac 14\) startet:
\(P(\text{Schütze 2 erlegt Hasen} ) = \frac 14p_2 = \boxed{\frac 4{23}}\).
Analog erhält man nebenbei:
\(P(\text{Schütze 3 erlegt Hasen} ) = \frac 1{12}p_3 = \frac 1{23}\).
Nachtrag:
Hier ist das Ergebnis einer kleinen Simulation mit 5000 Jagden und darunter die theoretischen Wahrscheinlichkeiten zum Vergleich:
