Wie berechnet man die Fourier_Transformierte dieser Funktion?

Question

Aufgabe:

Wie berechnet man die Fourier_Transformierte dieser Funktion?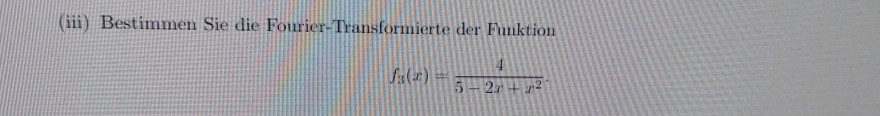

Text erkannt:

(iii) Bestimmen Sie die Fourier-Transformierte der Funktion
$f_{3}(x)=\frac{4}{5-2 x+x^{2}}$

Problem/Ansatz:

Ich kenne die Formel dafür aber das Problem ist, dass man diese Funktion nicht integrieren kann. Muss man hier irgendwie quadratisch ergänzen, und wenn ja wie?

Comments

Kann es sein, dass Du den Residuensatz aus der Funktionentheorie verwenden kannst / sollst?

---

hör zum ersten mal von dem satz. Wie würde es mit dem Satz funktionieren?

---

.. dass man diese Funktion nicht integrieren kann.

kann man schon! Es ist$$5-2 x+x^{2} = (x-1)^2 + 4 = 4\left(\left(\frac{x-1}{2}\right)^2 + 1\right)$$Damit kann man $f_3$ schreiben als$$\implies f_{3}(x) = \frac{1}{\left(\frac{x-1}{2}\right)^2 + 1}$$und mit der Substitution$$u = \frac{x-1}{2} \quad \frac{\text{d}u}{\text{d}x} = \frac{1}{2} \implies \text{d}x = 2 \text{d}x$$lässt sich das Integral bestimmen$$\begin{aligned} \int \frac{1}{\left(\frac{x-1}{2}\right)^2 + 1}\text{d}x &= 2\int \frac{1}{u^2+1}\,\text{d}u\\ &= 2\arctan(u) + C \\ &= 2\arctan\left(\frac{x-1}{2}\right) + C \\ \end{aligned}$$

---

@ rudstar: Wenn Due "Residuensatz" noch nie gehört hast, ist es zu kompliziert, das zu erklären. Dann nimm einfach das Ergebnis von Integralrechner o.ä.